关于 SVM（支持向量机），网上教程实在太多了，但真正能把内容讲清楚的少之又少。这段时间在网上看到一个老外的 svm 教程，几乎是我看过的所有教程中最好的。这里打算通过几篇文章，把我对教程的理解记录成中文。另外，上面这篇教程的作者提供了一本免费的电子书，内容跟他的博客是一致的，为了方便读者，我把它上传到自己的博客中。
这篇文章主要想讲清楚 SVM 的目标函数，而关于一些数学上的优化问题，则放在之后的文章。
论文笔记：Image Smoothing via L0 Gradient Minimization
今天要分享的这篇论文是我个人最喜欢的论文之一，它的思想简单、巧妙，而且效果还相当不错。这篇论文借助数学上的 \(L_0\) 范数工具对图像进行平滑，同时保留重要的边缘特征，可以实现类似水彩画的效果（见下图）。
另外这篇论文的作者徐立也是一个相当高产的研究员。
CNN的反向传播
在一般的全联接神经网络中，我们通过反向传播算法计算参数的导数。BP 算法本质上可以认为是链式法则在矩阵求导上的运用。但 CNN 中的卷积操作则不再是全联接的形式，因此 CNN 的 BP 算法需要在原始的算法上稍作修改。这篇文章主要讲一下 BP 算法在卷积层和 pooling 层上的应用。
PCA，到底在做什么
很久以前写过一篇 PCA 的小白教程，不过由于当时对 PCA 的理解流于表面，所以只是介绍了一下 PCA 的算法流程。今天在数图课上偶然听到 PCA 在图像压缩上的应用，突然明白了一点实质性的东西，这里趁热记录一波。
论文笔记：Deep feature learning with relative distance comparison for person re-identification
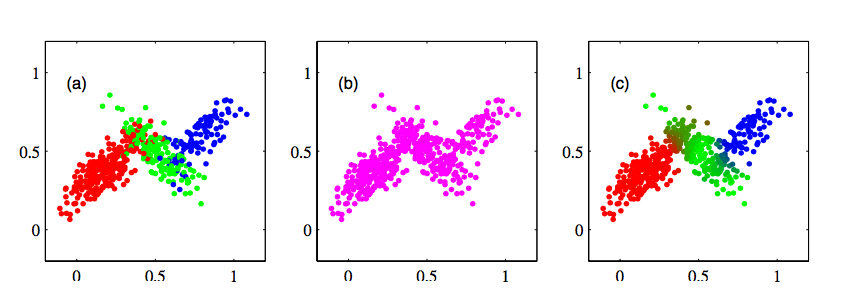
这篇论文是要解决 person re-identification 的问题。所谓 person re-identification，指的是在不同的场景下识别同一个人（如下图所示）。这里的难点是，由于不同场景下的角度、背景亮度等等因素的差异，同一个人的图像变化非常大，因而不能使用一般的图像分类的方法。论文采用了一种相似性度量的方法来促使神经网络学习出图像的特征，并根据特征向量的欧式距离来确定相似性。除此之外，论文通过对网络的训练过程进行分析，提出了一种计算效率更高的模型训练方法。
论文笔记：Cross-Domain Visual Matching via Generalized Similarity Measure and Feature Learning
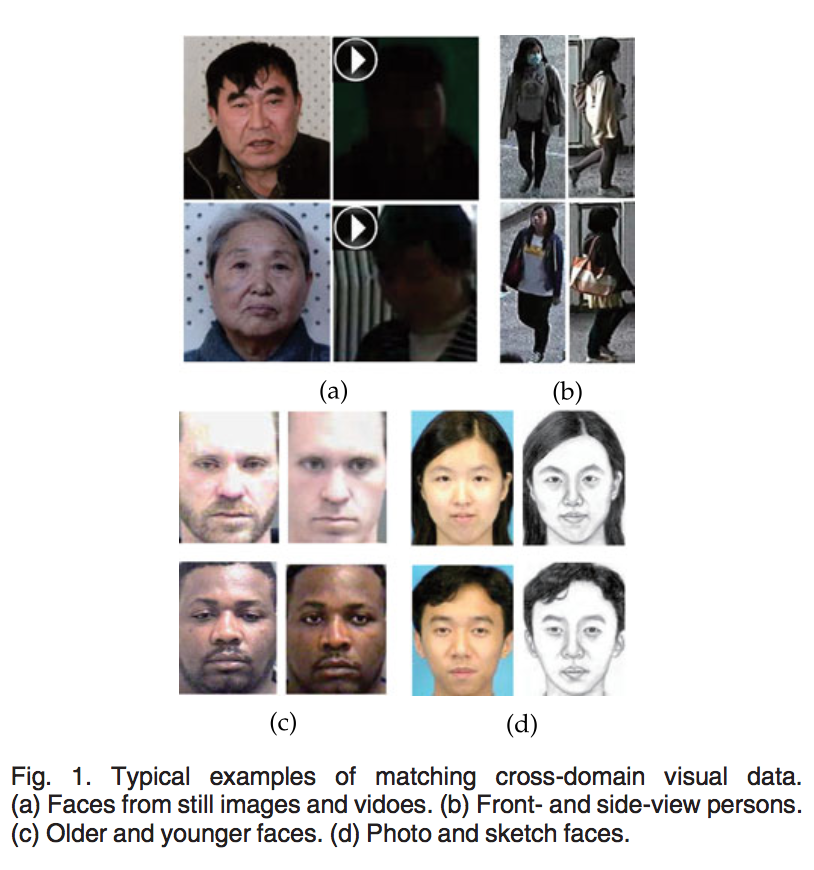
Cross-Domain Visual Matching，即跨域视觉匹配。所谓跨域，指的是数据的分布不一样，简单点说，就是两种数据「看起来」不像。如下图中，（a）一般的正面照片和各种背景角度下拍摄的照片；（b）摄像头不同角度下拍到的照片；（c）年轻和年老时的人脸照；（d）证件照和草图风格的人脸照，这些图像都存在对应关系，但由于它们属于不同的域，因此必须针对不同的域采用不同的特征提取方法，之后再做特征匹配。这篇论文提出用一种通用的相似模型来匹配两个域之间的特征，并将其和特征提取流程融合在一起，统一成一个 end-to-end 的框架。
word2vec概述
既然是概述，那么我也只会在文中谈一点关于 Word2Vec 的思想和大概的方法。对于这个算法，如果一开始学习就深入到算法细节中，反而会陷入局部极值点，最后甚至不知道这个算法是干嘛的。在了解算法大概的思路后，如果有进一步研究的必要，再去深究算法细节，这时一切都是水到渠成的。
先申明，由于我不是做 NLP 相关的，因此本文参考的主要是文末提供的博客，在算法理解上有很多不成熟的地方，还请见谅。
GMM与EM共舞
GMM，即高斯混合模型（Gaussian Mixture Model），简单地讲，就是将多个高斯模型混合起来，作为一个新的模型，这样就可以综合运用多模型的表达能力。EM，指的是均值最大化算法（expectation-maximization），它是一种估计模型参数的策略，在 GMM 这类算法中应用广泛，因此，有时候人们又喜欢把 GMM 这类可以用 EM 算法求解的模型称为 EM 算法家族。
这篇文章会简单提一下 GMM 模型的内容，最主要的，还是讲一下 EM 算法如何应用到 GMM 模型的参数估计上。
多维高斯分布
高中的时候我们便学过一维正态（高斯）分布的公式： \[ N(x|u,\sigma^2)=\frac{1}{\sqrt{2\pi \sigma^2}}exp[-\frac{1}{2\sigma^2}(x-u)^2] \] 拓展到高维时，就变成： \[ N(\overline x | \overline u, \Sigma)=\frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma|^{1/2}}exp[-\frac{1}{2}(\overline x-\overline u)^T\Sigma^{-1}(\overline x-\overline u)] \] 其中，\(\overline x\) 表示维度为 D 的向量，\(\overline u\) 则是这些向量的平均值，\(\Sigma\) 表示所有向量 \(\overline x\) 的协方差矩阵。
本文只是想简单探讨一下，上面这个高维的公式是怎么来的。
图像中的傅立叶变换（三）
在之前的文章中，我们介绍了傅立叶变换的本质和很多基本性质，现在，该聊聊代码实现的问题了。
为了方便起见，本文采用的编程语言是 Python3，矩阵处理用 numpy，图像处理则使用 OpenCV3。