关于 SVM(支持向量机),网上教程实在太多了,但真正能把内容讲清楚的少之又少。这段时间在网上看到一个老外的 svm 教程,几乎是我看过的所有教程中最好的。这里打算通过几篇文章,把我对教程的理解记录成中文。另外,上面这篇教程的作者提供了一本免费的电子书,内容跟他的博客是一致的,为了方便读者,我把它上传到自己的博客中。
这篇文章主要想讲清楚 SVM 的目标函数,而关于一些数学上的优化问题,则放在之后的文章。

什么是 SVM
SVM 的全称是 Support Vector Machine,中文名支持向量机。
关于 SVM 是什么这个问题,知乎上有一篇通俗易懂的文章,说到底,SVM 的提出主要是为了解决二分类的问题。下面会从最简单的数学入手,一步步揭开 SVM 的面纱。
超平面
什么是超平面
在正式开讲之前,需要先讲一下超平面(hyperplane)的概念,这是 SVM 中一个相当重要的概念。
在初中的时候,我们就知道 \(ax+b-y=0\) 表示的是一条直线。在机器学习里面,为了方便用向量的形式来表示,我们一般用 \(x_1\) 来代替 \(x\),\(x_2\) 来代替 \(y\),这样,直线就表示成了 \(\mathbf{w}^T\mathbf{x}+b=0\),其中 \(\mathbf{w}=\begin{bmatrix} a & -1 \end{bmatrix}^T\),\(\mathbf{x}=\begin{bmatrix} x_1 & x_2 \end{bmatrix}^T\)。
如果我们把目光投到三维:\(ax_1+bx_2+cx_3+d=0\),那么原来的直线就变成了一个平面。如果继续将维度升高到四维、五维。。。这时,平面就变成了高维空间的超平面。机器学习中的问题基本都是在高维空间处理的。
不过,由于超平面没法用画图表示,因此本文会使用二维的例子来介绍。
如果你看了上面知乎那篇文章,你就会知道,SVM 正是借助这个超平面来划分数据的。
关于这个超平面,我们要知道三点:
- 超平面也是由一系列点组成的。在线性代数中通常将点称为向量。如果点 \(\mathbf{x}\) 在超平面上,则满足 \(\mathbf{w}^T\mathbf{x}+b=0\)。由于这个超平面把数据分为两类,因此这些点又被称为支持向量。
- 假设超平面两侧各有一点 \(\mathbf{x_1}\) 和 \(\mathbf{x_2}\),则满足 \(\mathbf{w}^T\mathbf{x_1}+b>0\),\(\mathbf{w}^T\mathbf{x_2}+b<0\)。在二维中这一点很明显。
- \(\mathbf{w}\) 与超平面垂直。这一点是根据超平面的定义得来的,可以参看这个数学讲义。当然,如果实在无法理解,可以令 \(b=0\),这样超平面就变成 \(\mathbf{w}^T\mathbf{x}=0\),两向量内积为 0,证明 \(\mathbf{w} \perp \mathbf{x}\)。在 SVM 中,正样本的标签通常记为 1,负样本记为 -1。因此,为了保持符号上的一致性,规定 \(\mathbf{w}\) 的方向指向正样本的一侧。这样,如果 \(\mathbf{x_1}\) 是一个正样本,那么 \(\mathbf{w}^T\mathbf{x_1}+b>0\),否则 \(\mathbf{w}^T\mathbf{x_1}+b<0\)。
间距 margin
间距是 SVM 中另一个核心概念。间距指的就是点和超平面之间的距离。当样本点很多时,我们取样本点和超平面之间的最小距离作为间距。
SVM 的目标
SVM 的目的其实就是找一个区分数据最合适的超平面,超平面一侧是正样本,另一侧是负样本。我们应该能隐约感觉到:最合适的平面就在正负样本「最中间」的位置。换句话说,就是找一个间距最大的超平面。这样找到的超平面也将在正负样本的最中间,因为如果超平面离任何样本太近,间距都会变小,因此为了保证间距最大,就必须与所有正负样本都足够的远。
如何找到最合适的超平面
假设下图中的 A~G 表示样本点,橙色线是超平面,两条蓝线表示与超平面平行的面,它们划定了超平面的间距(注意右侧的蓝线穿过了离超平面最近的 A、B 两点)。
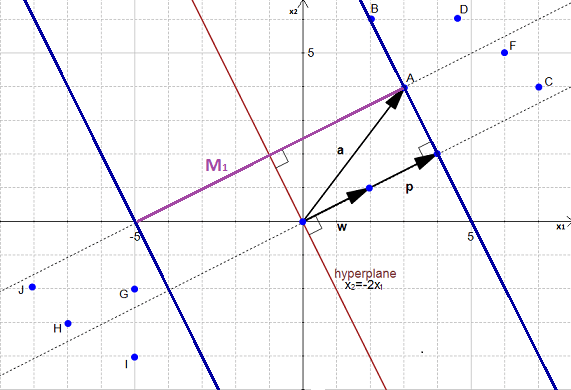
虽然这个超平面能把正负样本点分开,但显然不是最优的超平面,因为我们可以找到一个新的超平面,使间距更大(由 \(\frac{M_1}{2}\) 扩大到 \(\frac{M_2}{2}\))。
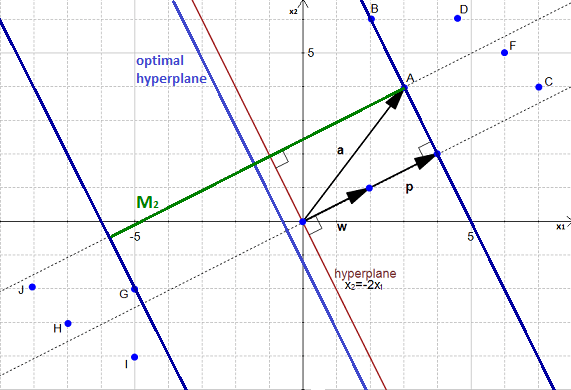
到这里,我们可以发现,超平面是否合适,跟间距大小息息相关。因此,寻找最优的超平面,就等价于找到最大的间距。
寻找最大间距
下面就来讨论一下怎么找到最大的间距。
假设我们有一个样本集 \(D=\{(\mathbf{x_i},y_i)\ \big |\ \mathbf{x_i} \in R^p, y_i \in \{-1,1\}\}\),\(y_i\) 表示样本标签,正样本取 1,负样本取 -1。
为了计算超平面 \(\mathbf{w}^T\mathbf{x}+b=0\) 的间距,我们可以仿照上图中的蓝线,引入两个超平面: \(\mathbf{w}^T\mathbf{x}+b=\delta\) 和 \(\mathbf{w}^T\mathbf{x}+b=-\delta\)(\(\delta\) 取正数)。注意,这两个超平面之间不能有任何数据点。因此,他们要满足一个限制条件:对于正样本(\(y_i=1\))而言,\(\mathbf{w}^T\mathbf{x}+b\ge \delta\),对于负样本(\(y_i=-1\)),\(\mathbf{w}^T\mathbf{x}+b\le -\delta\)。这样一来,求原超平面的间距就转换为求这两个超平面之间的距离。利用标签的正负号,我们可以把两个超平面的限制条件统一为: \[ y_i(\mathbf{w}^T\mathbf{x_i}+b) \ge \delta \tag{1} \] 接下来要考虑如何计算这两个超平面之间的距离。
在高中阶段,我们就学过如何计算两条平行直线之间的距离,这里完全可以把二维的公式拓展到高维。不过,这里我们还是从向量的角度出发,看看如何计算两个超平面之间的距离。
假设这两个超平面分别为 \(H_0: \mathbf{w}^T\mathbf{x}+b=-\delta\) 和 \(H_1: \mathbf{w}^T\mathbf{x}+b=\delta\),\(x_0\) 是 \(H_0\) 上一点,两个平面之间的距离是 \(m\)。
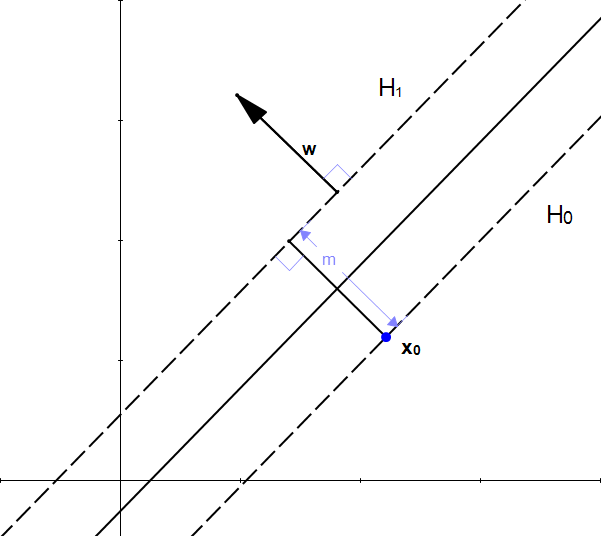
为了计算 \(m\),需要找一个跟 \(m\) 相关的表达式。假设 \(H_1\) 上有一点 \(x_1\),使得向量 \(\overline {x_0x_1} \perp H_1\),则 \(\mathbf{x_1}=\mathbf{x_0}+\overline {x_0x_1}\)。想要求 \(\overline {x_0x_1}\),我们需要确定它的方向和长度。在之前介绍超平面时,我们已经知道,\(\mathbf{w} \perp H_1\),所以这个向量的方向应该和 \(\mathbf{w}\) 相同,而它的长度就是我们要求的 \(m\),所以 \(\overline {x_0x_1}=m\frac{\mathbf{w}}{||\mathbf{w}||}\),既而 \(\mathbf{x_1}=\mathbf{x_0}+m\frac{\mathbf{w}}{||\mathbf{w}||}\)。
现在把 \(\mathbf{x_1}\) 代入 \(H_1 (\mathbf{w}^T\mathbf{x}+b=\delta)\) 中: \[ \begin{align} \mathbf{w}^T\mathbf{x_1}+b=&\mathbf{w}^T(\mathbf{x_0}+m\frac{\mathbf{w}}{||\mathbf{w}||})+b \notag \\ =&\mathbf{w}^T\mathbf{x_0}+m\frac{\mathbf{w}^T\mathbf{w}}{||\mathbf{w}||}+b \tag{2} \\ =&\delta \notag \end{align} \] 由于 \(\mathbf{x_0}\) 是 \(H_0\) 上一点,所以 \(\mathbf{w}^T\mathbf{x_0}+b=-\delta\),代入(2)式: \[ \begin{align} \mathbf{w}^T\mathbf{x_1}+b=&-\delta+m\frac{\mathbf{w}^T\mathbf{w}}{||\mathbf{w}||} \notag \\ =&-\delta + m||\mathbf{w}|| \notag \\ =&\delta \notag \end{align} \] 这样我们就得到 \(m\) 的表达式: \[ m=\frac{2\delta}{||\mathbf{w}||} \tag{3} \] 考虑到 \(\delta\) 是一个正数,因此,要使 \(m\) 最大,就必须让 \(||\mathbf{w}||\) 最小。再考虑到两个超平面的限制条件(1),我们就可以得到如下 SVM 的目标函数。
目标函数
综合考虑 (2) (3),我们得到 SVM 最终的目标函数: \[ \underset{(\mathbf{w},b)}{\operatorname{min}} ||\mathbf{w}|| \ \ \ \ \operatorname{s.t.} \ y_i(\mathbf{w}^T\mathbf{x_i}+b) \ge \delta, \ \ i=1,...,m \] 找出使这个函数最小的 \(\mathbf{w}\) 和 \(b\),就找到了最合适的超平面。注意,由于我们有 \(m\) 个样本,所以总共有 \(m\) 个限制条件。