上一篇文章讲了傅立叶变换的本质。这篇文章会总结一下傅立叶变换的常用性质，公式巨多，慎入！慎入！

关于傅立叶变换，知乎上已经有一篇很好的教程，因此，这篇文章不打算细讲傅立叶的物理含义，只是想从图像的角度谈一谈傅立叶变换的本质和作用。

本文假设读者已经熟知欧拉公式： \[ e^{j\pi x}=\cos{\pi x}+j\sin{\pi x} \] 并且知道高数课本中给出的傅立叶变换公式： \[ f(x) ～ \frac{a_0}{2}+\sum_{n=1}^{\infty}{[a_n \cos{nx}+b_n\sin{nx}]} \] 其中 \(a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}{f(x)\cos{nx}}dx\)，\(b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}{f(x)\sin{nx}}dx\)。

当然，线性代数也还是要懂一些的。

在讨论最大似然估计之前，我们先来解决这样一个问题：有一枚不规则的硬币，要计算出它正面朝上的概率。为此，我们做了 10 次实验，得到这样的结果：[1, 0, 1, 0, 0, 0, 0, 0, 0, 1]（1 代表正面朝上，0 代表反面朝上）。现在，要根据实验得到的结果来估计正面朝上的概率，即模型的参数 \(p\)（\(0 \le p \le 1\)）。

当然，对于投硬币这种问题，由于模型很简单，我们可以用大量实验来近似最终结果，不过，如果事件模型复杂一些，做大量的实验就显得不太现实。这个时候，用最大似然估计的思想，则可以通过较少的实验得出一个相对好的结果。本文就从这个简单的例子出发，对最大似然估计做一次简单的描述。

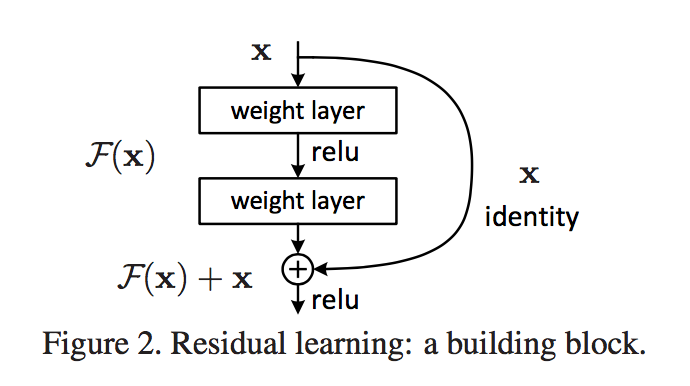
之前提到，深度神经网络在训练中容易遇到梯度消失/爆炸的问题，这个问题产生的根源详见之前的读书笔记。在 Batch Normalization 中，我们将输入数据由激活函数的收敛区调整到梯度较大的区域，在一定程度上缓解了这种问题。不过，当网络的层数急剧增加时，BP 算法中导数的累乘效应还是很容易让梯度慢慢减小直至消失。这篇文章中介绍的深度残差 (Deep Residual) 学习网络可以说根治了这种问题。下面我按照自己的理解浅浅地水一下 Deep Residual Learning 的基本思想，并简单介绍一下深度残差网络的结构。

在神经网络的训练过程中，总会遇到一个很蛋疼的问题：梯度消失/爆炸。关于这个问题的根源，我在上一篇文章的读书笔记里也稍微提了一下。原因之一在于我们的输入数据（网络中任意层的输入）分布在激活函数收敛的区域，拿 sigmoid 函数举例：

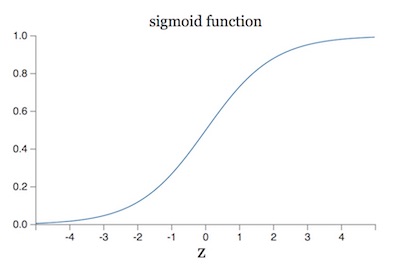
如果数据分布在 [-4, 4] 这个区间两侧，sigmoid 函数的导数就接近于 0，这样一来，BP 算法得到的梯度也就消失了。

之前的笔记虽然找到了原因，但并没有提出解决办法。最近在实战中遇到这个问题后，束手无策之际，在网上找到了这篇论文 Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift。原来早在 2015 年就有人提出了解决方案，而且基本已经成为神经网络的组成部分之一了。本文仅仅是对这篇论文做一些梳理，并总结一些我个人的理解。论文中还有很多不解的地方，因此总结的过程中难免存在错误，还请发现的同学指正☺️

(本文是根据 neuralnetworksanddeeplearning 这本书的第五章Why are deep neural networks hard to train? 整理而成的读书笔记，根据个人口味做了删减)

在之前的笔记中，我们已经学习了神经网络最核心的 BP 算法，以及一些改进的方案（如：引入交叉熵函数）来提高网络训练的速度。但如果仔细思考会发现，前面例子中的网络都很「浅」，最多就一两个隐藏层，而一旦网络层数增加，有很多问题将不可避免地暴露出来。今天，我们就来认识一个最蛋疼的问题：深度神经网络非常难训练。

本文是根据 TensorFlow 官方教程翻译总结的学习笔记，主要介绍了在 TensorFlow 中如何共享参数变量。

教程中首先引入共享变量的应用场景，紧接着用一个例子介绍如何实现共享变量（主要涉及到 tf.variable_scope()和tf.get_variable()两个接口），最后会介绍变量域 (Variable Scope) 的工作方式。

(本文是根据 neuralnetworksanddeeplearning 这本书的第三章Improving the way neural networks learn整理而成的读书笔记，根据个人口味做了删减)

上一章，我们介绍了神经网络容易出现的过拟合问题，并学习了最常用的正则化方法，以及其他一些技巧，今天，我们将介绍本章节最后两个问题：权重初始化和超参数的选择

最近在学习 SVM 的过程中，遇到关于优化理论中拉格朗日乘子法的知识，本文是根据几篇文章总结得来的笔记。由于是刚刚接触，难免存在错误，还望指出😁。另外，本文不会聊到深层次的数学推导，仅仅是介绍拉格朗日乘子法的内容，应用，以及个人对它的感性理解。

什么是拉格朗日乘子法

按照维基百科的定义，拉格朗日乘数法是一种寻找多元函数在其变量受到一个或多个条件的约束时的极值的方法。用数学式子表达为： \[ \underset{x, y} {\operatorname {minimize}} f(x, y) \\ \operatorname{subject\ to} g(x, y) = c \] 简单理解就是，我们要在满足 \(g(x, y)=c\) 这个等式的前提下，求 \(f(x, y)\) 函数的最小值（最大值道理相同）。这样的问题我们在高中的时候就遇到过了，只不过高中时遇到的限制条件 \(g(x, y)=c\) 都比较简单，一般而言都可以将 \(y\) 用 \(x\) 的式子表示出来，然后用变量替换的方法代回 \(f(x, y)\) 求解。但是，如果 \(g(x, y)\) 的形式过于复杂，或者变量太多时，这种方法就失效了。而拉格朗日乘子法就是解决这类问题的通用策略。

(本文是根据 neuralnetworksanddeeplearning 这本书的第三章Improving the way neural networks learn整理而成的读书笔记，根据个人口味做了删减)

上一章，我们学习了改善网络训练的损失函数：交叉熵函数。今天要介绍神经网络容易遇到的过拟合（overfitting）问题，以及解决的方法：正则化（regularization）。