(本文是根据 neuralnetworksanddeeplearning 这本书的第五章Why are deep neural networks hard to train? 整理而成的读书笔记,根据个人口味做了删减)
在之前的笔记中,我们已经学习了神经网络最核心的 BP 算法,以及一些改进的方案(如:引入交叉熵函数)来提高网络训练的速度。但如果仔细思考会发现,前面例子中的网络都很「浅」,最多就一两个隐藏层,而一旦网络层数增加,有很多问题将不可避免地暴露出来。今天,我们就来认识一个最蛋疼的问题:深度神经网络非常难训练。
网络越深效果越好
近几年的研究已经表明,网络的层数越深,模型的表达能力就越强。在图像识别中,网络的第一层学会如何识别边缘,第二层在第一层的基础上学会如何识别更复杂的形状,如三角形等,然后第三层又继续在第二层的基础上学会识别出更复杂的形状。如此往复,最后网络便学会识别出更高级的语义信息。这也是为什么深度学习近几年能取得突破的,因为深度神经网络的表达能力实在太强了。
不过,在训练深度神经网络的过程中,人们也遇到一个严重的问题:当后面层的网络飞快训练时,前面层的网络却「僵住」了,参数不再更新;有时候,事情又刚好相反,前面层的网络训练飞快,后面层的网络却收敛了。
通过本节的学习,我们将了解这一切背后的深层原因。
消失的梯度
沿袭之前 MNIST 的例子,我们先做几组实验,来看看什么是梯度消失。
这几组实验中,我们的网络结构分别如下:
1 | net = network2.Network([784, 30, 10]) |
这几个网络的唯一区别是,每一个网络都比前面的多了一个包含 30 个神经元的隐藏层。实验中,其他参数,包括训练数据完全一样。在 MNIST 数据集上,得出这四个实验的准确率分别为:96.48%,96.90%,96.57%,96.53%。
看得出来,第二个网络训练的结果比第一个好一些,但当隐藏层继续增加时,效果反而下降了。这让我们很惊奇,不是说网络层数越深,效果越好吗?况且,即使中间的网络什么都没有学习到,也总不至于其负作用吧。
为了进一步了解背后的原因,我们打算跟踪一下网络的参数,确认网络是否真的得到训练。
简单起见,我们分析一下第二个网络 ([784, 30, 30, 10]) 中两个隐藏层的梯度。下图演示了当训练开始时,这两个层里面每个神经元的梯度值,为了方便,只摘取了前六个神经元:
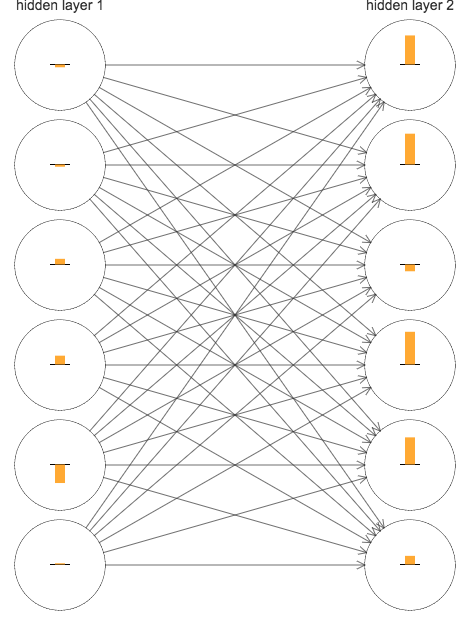
图中神经元上的柱状图表示梯度值 \(\partial C/ \partial b\),在 BP 的四个公式中,我们知道:\(\frac{\partial C}{\partial b_j^{l}}=\delta_j^l \tag{BP3}\) \(\frac{\partial C}{\partial w_{jk}^{l}}=a_{k}^{l-1}\delta_{j}^{l} \tag{BP4}\)
所以,柱状图表示的除了是偏差 bias 的梯度外,也多少可以反应权重 weights 的梯度。
由于权重的初始化是随机的,所以每个神经元的梯度都有所不同,不过很明显的一点是,第 2 个隐藏层的梯度总体上比第 1 个隐藏层要大,而梯度越大,学习速度也相对的越快。
为了探究这是否是偶然(也许这两层中后面的神经元会不同呢),我们决定用一个全局的梯度向量 \(\delta\) 来比较这两个隐藏层参数的总体梯度情况。我们定义 \(\delta_j^l=\partial C/ \partial b_j^l\),所以你可以把 \(\delta\) 看作是上图中所有神经元梯度的向量。我们用向量长度 \(||\delta^i||\) 来代表每 i 个隐藏层的学习速度。
当只有两个隐藏层时(即上图),\(||\delta^1||=0.07\)、\(||\delta^2||=0.31\),这进一步验证了:第二个隐藏层的学习率高于第一个隐藏层。
如果有三个隐藏层呢?结果是:\(||\delta^1||=0.012\)、\(||\delta^2||=0.060\)、\(||\delta^3||=0.283\)。同样的,后面的隐藏层学习速度都比前面的要高一些。
有人可能会说,以上的梯度都是在刚开始训练后某个时刻计算得到的,在网络训练过程中,这些梯度又是否会进一步提升呢?为了解答这个问题,我们计算出之后更多轮学习后的梯度,并绘制成下面的曲线图:
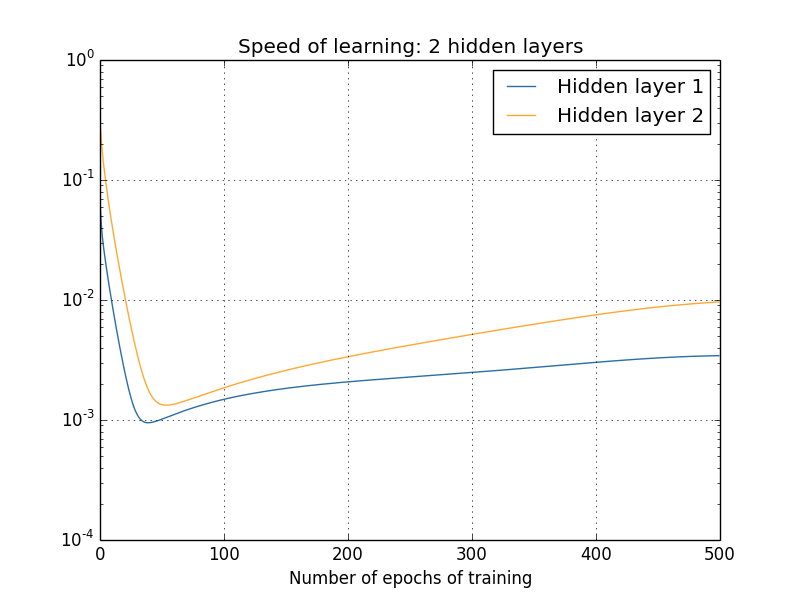
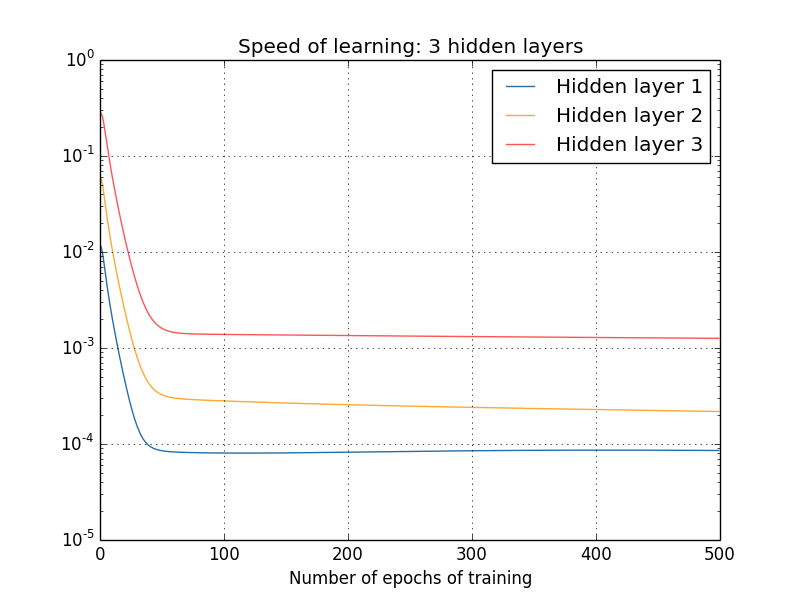
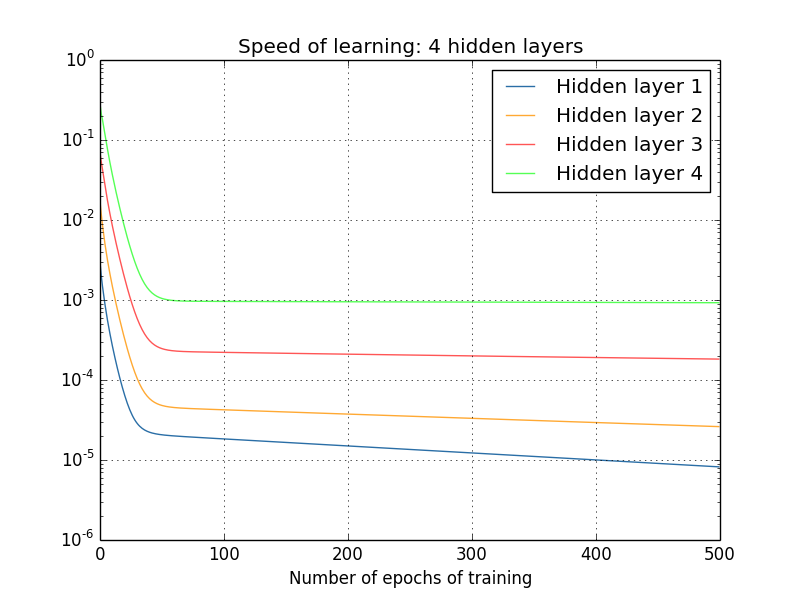
显而易见地是,不管隐藏层有多少,后面层的学习速度都比前一层要高 5 到 10 倍,这样一来,第一个隐藏层的学习速度甚至只有最后一层的百分之一,当后面的参数正大踏步训练的时候,前面层的参数就基本停滞不前了。这种现象,就叫做梯度消失。梯度消失并不意味着网络已经趋于收敛,因为在实验中,我们特意在训练开始时计算出了梯度,对于一个参数随机初始化的网络,要想在刚开始时就让网络趋于收敛,这几乎是不可能的,因此我们认为梯度消失并不是网络收敛引起的。
另外,随着研究深入,我们也会发现,有时候前面层的梯度虽然没有消失,但却变得很大,几乎是后面层的成百上千倍,导致出现了 NaN,简直「爆炸」了。对于这种情况,我们又称之为梯度爆炸。
不管是梯度消失还是爆炸,都是我们不愿看到的。下面我们需要进一步研究这种现象产生的原因,并想办法解决它。
梯度消失的原因
这一节,我们来探讨一下:为什么网络的梯度会消失?或者说,为什么深度神经网络的梯度会如此不稳定。
简单起见,我们来分析一个只有一个神经元的网络:

\(b\) 和 \(w\) 表示参数,\(C\) 是损失函数,激活函数采用 sigmoid,每层网络的输出为 \(a_j=\sigma(z_j)\),\(z_j=w_ja_{j-1}+b_j\)。
下面,我们要求出 \(\partial C/\partial b_1\),看看是什么原因导致这个值很小。
根据 BP 的公式可以推出:

这个公式看起来略微比较复杂,不急,我们来看看它是怎么来的。由于网络十分简单(只有一条链),所以我们准备从另一个更形象的角度来推出这个式子(BP 也是完全可以推出该式子的)。
假设有一个增量 \(\Delta b_1\) 出现,由于 \(a_1=\sigma(z_1)=\sigma(w_1a_0+b_1)\),可以推出:
\(\Delta a_1 \approx \frac{\partial \sigma((w_1\ a_0+b_1)}{\partial b_1} \Delta b_1=\sigma'(z_1)\Delta b_1\)(注意 \(\Delta a_1\) 不是导数,而是由 \(\Delta b_1\) 引起的增量,所以是斜率乘以 \(\Delta b_1\))。
然后进一步的,\(\Delta a_1\) 又会引起 \(z_2\) 的变化,根据 \(z_2=w_2 a_1+b_2\) 可以得出:
\(\Delta z_2 \approx \frac{\partial z_2}{\partial a_1}\Delta a_1=w_2 \Delta a_1\)。
将之前 \(\Delta a_1\) 的公式代入上式就可以得到:
\(\Delta z_2 \approx \sigma'(z_1)w_2 \Delta b_1\)。
可以看出,这个式子和我们最开始的式子已经很相似了。之后,我们依葫芦画瓢不断往后计算,就可以得到 \(C\) 的增量:
\(\Delta C \approx \sigma'(z_1)w_2 \sigma'(z_2) \ldots \sigma'(z_4) \frac{\partial C}{\partial a_4} \Delta b_1 \tag{120}\)
除以 \(\Delta b_1\) 后,就可以得到最开始的等式:
\(\frac{\partial C}{\partial b_1} = \sigma'(z_1) w_2 \sigma'(z_2) \ldots\sigma'(z_4) \frac{\partial C}{\partial a_4}.\tag{121}\)
为什么梯度会消失
有了上面这个式子做铺垫,你是否已经猜出了梯度消失的原因。没错,就跟 \(0.9^n \approx 0\) 道理一样。
首先,我们回顾一下 \(\sigma'()\) 函数的图像:
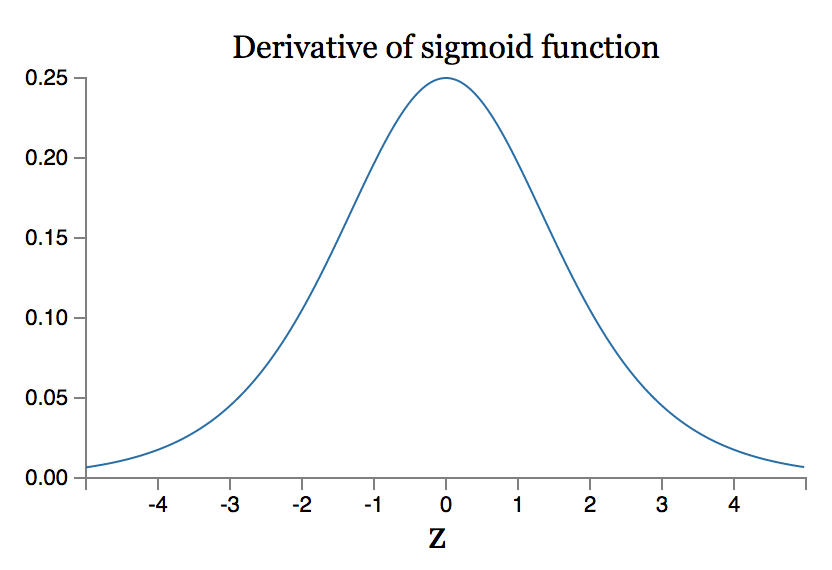
这个函数最大值才 1/4。加上我们的参数 \(W\) 是根据均值为 0,标准差为 1 的高斯分布初始化的,即 \(|w_j|<1\) ,所以\(|w_j \sigma'(z_j)<1/4|\)。这些项累乘起来,最后的结果就会越来越小。再注意看下面这幅图,由于不同隐藏层的导数累乘的数量不同,因此对应的梯度也就有了高低之分。
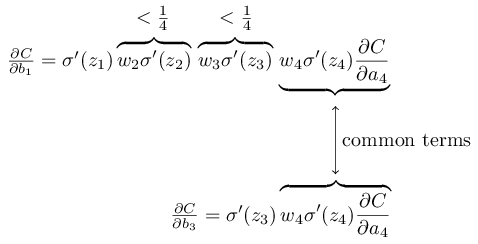
以上的推导虽然不是很正式,但它已经足够阐明问题的根源。
梯度爆炸的问题这里就不再赘述了,原理和梯度消失一样,当每一项的值都大于 1 时,累乘起来就会变得很大。
记得在之前的学习笔记的最后,我曾经提出一个问题:尽管交叉熵函数解决了网络学习速度下降的问题,但它针对的只是最后一层,对于前面的隐藏层,学习速度依然可能下降。作者之前之所以避而不谈这个问题,是因为之前针对的网络层数都很少,而本文中也已经显示地点出并分析了问题的根源。
复杂网络中的梯度同样不稳定
上面的例子中我们只是用了一个简单的例子来解释原因,在更复杂的网络中,我们仍然可以用类似的方法解释梯度的不稳定现象。
例如,对于下面这个复杂的网络:
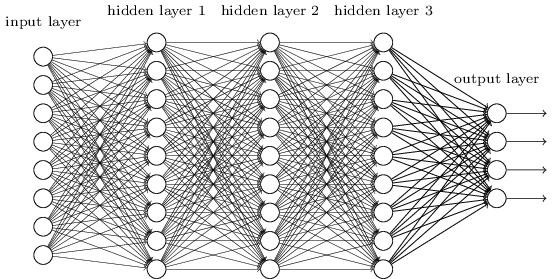
我们可以借助 BP 公式推出: \[ \begin{eqnarray} \delta^l = \Sigma'(z^l) (w^{l+1})^T \Sigma'(z^{l+1}) (w^{l+2})^T \ldots \Sigma'(z^L) \nabla_a C \tag{124}\end{eqnarray} \] 这里面,\(\Sigma'(z^l)\) 是对角矩阵,矩阵对角线上的元素由 \(\sigma'(z)\) 的值构成。\(\nabla_a C\) 则是由 \(C\) 对 输出层求偏导后得来的向量。
这个式子尽管许多,但形式上依然是一样的,最后矩阵相乘的累积效应依然会导致梯度消失或者爆炸。
深度学习的其他障碍
虽然这一章中我们只是提到梯度不稳定的问题,但事实上,有很多研究显示:深度学习同样存在很多其他的障碍。
比如:激活函数的选择会影响网络的学习(参见论文:Understanding the difficulty of training deep feedforward neural networks)。
又比如:参数的初始化也会影响网络的训练(参见论文:On the importance of initialization and momentum in deep learning)。
可见,关于深度神经网络的训练障碍,目前还是一个复杂的问题,需要更进一步的研究。在下一章中,我们将继续学习一些深度学习的方法,这些方法在某种程度上,可以克服深度神经网络的这些学习障碍。