之前提到,深度神经网络在训练中容易遇到梯度消失/爆炸的问题,这个问题产生的根源详见之前的读书笔记。在 Batch Normalization 中,我们将输入数据由激活函数的收敛区调整到梯度较大的区域,在一定程度上缓解了这种问题。不过,当网络的层数急剧增加时,BP 算法中导数的累乘效应还是很容易让梯度慢慢减小直至消失。这篇文章中介绍的深度残差 (Deep Residual) 学习网络可以说根治了这种问题。下面我按照自己的理解浅浅地水一下 Deep Residual Learning 的基本思想,并简单介绍一下深度残差网络的结构。
基本思想
回到最开始的问题,为什么深度神经网络会难以训练?根源在于 BP 的时候我们需要逐层计算导数并将这些导数相乘。这些导数如果太小,梯度就容易消失,反之,则会爆炸。我们没法从 BP 算法的角度出发让这个相乘的导数链消失,因此,可行的方法就是控制每个导数的值,让它们尽量靠近 1,这样,连乘后的结果不会太小,也不会太大。
现在,我们就从导数入手,看看如何实现上面的要求。由于梯度消失的问题比梯度爆炸更常见,因此只针对梯度消失这一点进行改进。
假设我们理想中想让网络学习出来的函数是 \(F(x; {W_i})\),但由于它的导数 \(\frac{\partial F}{\partial x}\) 太小,所以训练的时候梯度就消失了。所谓太小,就是说 \(\frac{\partial F}{\partial x} \approx 0\),那么,我们何不在这个导数的基础上加上 1 或者减去 1,这样梯度不就变大了吗?(这里的 1 是为了满足之前提到的梯度靠近 1 这一要求,事实上,只要能防止梯度爆炸,其他数值也是可以的,不过作者在之后的实验中证明,1 的效果最好)
按照这种思路,我们现在想构造一个新的函数,让它的导数等于 \(\frac{\partial F}{\partial x}+1\)。由这个导数反推回去,很自然地就得到一个我们想要的函数:\(H(x)=F(x)+x\),它的导数为:\(\frac{\partial H}{\partial x} = \frac{\partial F}{\partial x}+1\)。这个时候你可能会想,如果将原来的 \(F(x)\) 变成 \(H(x)\),那网络想要提取的特征不就不正确了吗,这个网络还有什么用?不错,我们想要的最终函数是 \(F(x; {W_i})\),这个时候再加个 \(x\) 上去,结果肯定不是我们想要的。但是,为什么一定要让网络学出 \(F(x; {W_i})\)?为什么不用 \(H(x)\) 替换原本的 \(F(x;{W_i})\),而将网络学习的目标调整为:\(F(x)=H(x)-x\)?要知道,神经网络是可以近似任何函数的,只要让网络学出这个新的 \(F(x)\),那么我们自然也就可以通过 \(H(x)=F(x)+x\) 得到最终想要的函数形式。作者认为,通过这种方式学习得到的 \(H(x)\) 函数,跟当初直接让网络学习出的 \(F(x, {W_i})\),效果上是等价的,但前者却更容易训练。
==================== UPDATE 2018.1.23 =====================
时隔几个月重新看这篇文章,发现当初的理解存在一个巨大的问题,在此,对那些被我误导的同学深深道歉🙇。
这里的问题在于,BP 算法中我们要计算的是参数 \(W\) 和 \(b\) 的导数,所以导数的形式不应该是 \(\frac{\partial F}{\partial x}\),而是 \(\frac{F}{W_i}\)(bias 同理)。这样一来,我之前对残差网络改进梯度消失问题的理解就错了。不过,我依然固执地认为,残差学习是为了解决深度网络中梯度消失的问题,只是要换种方式理解。
对于最简单的神经网络(假设退化成一条链):
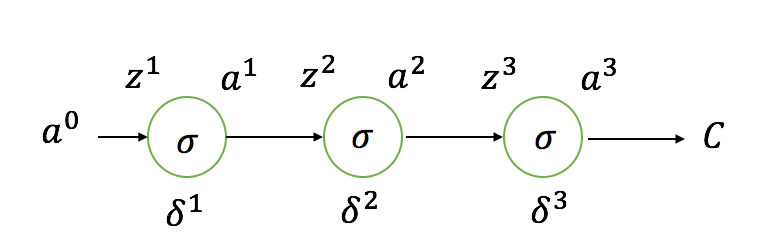
\(C\) 是网络的 loss 函数,\(z^l\) 表示第 l 层激活函数的输入,\(a^l\) 表示第 l 层激活函数的输出(\(a^0\) 就是网络最开始的输入了),则 \(a^l = \sigma(z^l)\),\(z^l=a^{l-1}*w^l\)(\(W^l\) 是第 l 层的权重参数,简单起见,不考虑 bias)。\(\delta^l\) 是第 l 层的误差。
根据 BP 算法,先计算误差项: \[ \delta^3=\frac{\partial C}{\partial a^3}\frac{\partial a^3}{\partial z^3}=\frac{\partial C}{\partial a^3}\sigma'(z^3) \\ \delta^2=\delta^3 \sigma'(z^2)w^3=\frac{\partial C}{\partial a^3}\sigma'(z^3)\sigma'(z^2)w^3 \\ \delta^1=\delta^2\sigma'(z^1)w^2=\frac{\partial C}{\partial a^3}\sigma'(z^3)\sigma'(z^2)w^3\sigma'(z^1)w^2 \] 然后根据误差项计算 \(w\) 的导数: \[ \frac{\partial C}{\partial w^3}=\delta^3a^2 \\ \frac{\partial C}{\partial w^2}=\delta^2a^1 \\ \frac{\partial C}{\partial w^1}=\delta^1a^0 \] 一般来说,梯度的消失是这些项的累乘造成的:\(\sigma'(z^3)\sigma'(z^2)w^3\sigma'(z^1)w^2\)(因为 \(\sigma'(z^l)\) 和 \(w^l\) 一般都小于 1)。
那残差网络做了那些修改呢?其实就是简单地在激活函数的输出后面,加入上一层的输入:
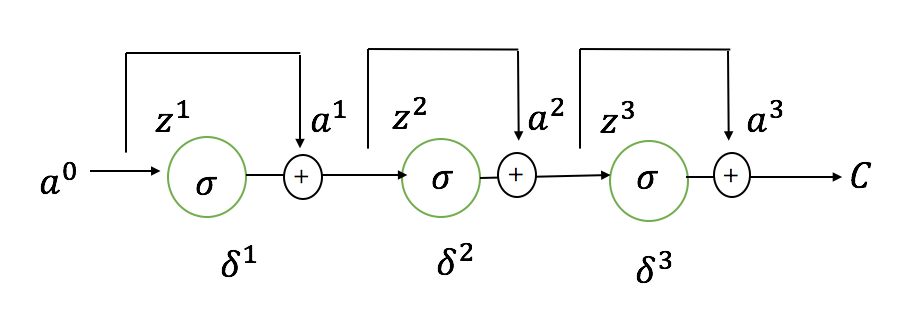
假设原本的网络是要学习一个 \(H(x)\) 函数,那现在这个网络依然是要学习 \(H(x)\)。只不过,原本的网络要学习的是整个 \(H(x)\),而残差网络中,和原本网络相同的那部分结构,要学习的就只是 \(H(x)-x\)。换句话说,它要学习的东西只是一个微小的变化,因此训练起来相对更容易一些。
另一方面,我们沿用之前对导数的分析思路,看看残差网络的梯度会发生什么变化。
首先,残差网络的前向传播发生了变化: \[ z^1=a^0 \\ a^1=\sigma(z^1)+a^0 \\ z^2=a^1w^2 \\ a^2=\sigma(z^2)+a^1 \\ z^3=a^2w^3 \\ a^3=\sigma(z^3)+a^2 \] 反向传播计算的误差项为: \[ \delta^3=\frac{\partial C}{\partial z^3}=\frac{\partial C}{\partial a^3}\frac{\partial a^3}{\partial z^3}=\frac{\partial C}{\partial a^3}[\sigma'(z^3)+\frac{\partial a^2}{\partial z^3}] \\ \delta^2=\delta^3 w^3 \frac{\partial a^2}{\partial z^2}=\frac{\partial C}{\partial a^3}[\sigma'(z^3)+\frac{\partial a^2}{\partial z^3}]w^3 [\sigma'(z^2)+\frac{\partial a^1}{\partial z^2}] \\ \vdots \] 由于 \(z^3=a^2w^3\),所以 \(a^2=\frac{z^3}{w^3}\),故 \(\frac{\partial a^2}{\partial z^3}=\frac{1}{w^3}\),同理 \(\frac{\partial a^1}{\partial z^2}=\frac{1}{w^2}\)。代入到上式中就变成: \[ \delta^3=\frac{\partial C}{\partial a^3}[\sigma'(z^3)+\frac{1}{w^3}] \\ \delta^2=\frac{\partial C}{\partial a^3}[\sigma'(z^3)+\frac{1}{w^3}]w^3 [\sigma'(z^2)+\frac{1}{w^2}]=\frac{\partial C}{\partial a^3}[\sigma'(z^3)w^3+1] [\sigma'(z^2)+\frac{1}{w^2}] \\ \vdots \] 对比之前没加残差结构的网络,这个新的网络结构中,误差项 \(\delta^l\) 减小为 0 的可能性降低了。以 \(\delta^2\) 为例,原本的 \(\delta^2=\frac{\partial C}{\partial a^3}\sigma'(z^3)\sigma'(z^2)w^3\),而现在,连乘的项变成了 \([\sigma'(z^3)w^3+1]\) 和 \([\sigma'(z^2)+\frac{1}{w^2}]\),由于 \(\sigma'(z^l)\) 和 \(w^l\) 一般都小于 1,所以这两项的值会略大于 1,这样,无论连乘多少项,梯度都不会缩小到 0。
==================================================
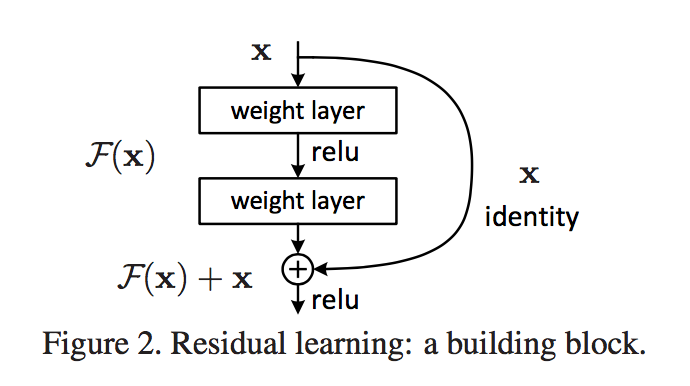
上面所说的 \(F(x)=H(x)-x\) 就是所谓的残差 (residual),而式子内的 \(x\) 在论文中被称为 Identity Mapping,因为 x 可以看作是由自己到自己的映射函数。基于此,我们可以得到一个新的网络结构,如同开篇的图片所示,这个网络结构跟普通的网络结构类似,但在输出那里多加了一个 Identity Mapping,相当于在网络原有输出的基础上加一个 x,这样便得到我们想要的函数 \(H(x)\)。作者将这种相加称为 shortcut connection,意思就是说,\(x\) 没有经过中间的变换操作,像「短路」一样直接跳到输出那里和 \(F(x)\) 相加。需要注意的是,这个网络结构的输入并不一定是原始的数据,它可以是前面一层网络的输出结果。同理,网络的输出也可以继续输入到后面层的网络中。
我们用一个式子来表示这个网络:\(y=F(x,{W_i})+x\),其中 \(F(x,{W_i})=W_2 \sigma(W_1x)\) (这里忽略了 bias)。在论文中,这里的 \(\sigma\) 函数采用的是 ReLu。得到 \(y\) 后,作者又对其做了一次 ReLu 操作,然后再进入下一层网络。
Talk is cheap,show you the code(这里用 tensorflow 表示一下上图那个网络结构):
1 | # 假设 x 是该网络结构的输入 |
因为 \(x\) 和 \(F(x)\) 是直接相加的,所以它们的维度必须相同,不同的情况下,需要对 \(x\) 的维度进行调整。可以通过做一次线性变换将它投影到所需的维度空间,也可以用其他简单粗暴的方法。比如,当维度太高时,可以用 pooling 的方法降低维度。而维度较低时,作者在实验中则是直接补 0 来扩展维度。
深度残差网络
好了,了解了残差网络的基本思路和简单的网络结构后,下面我们可以将它拓展到更深的网络结构中。
下图是一个普通的网络和改造后的残差网络:
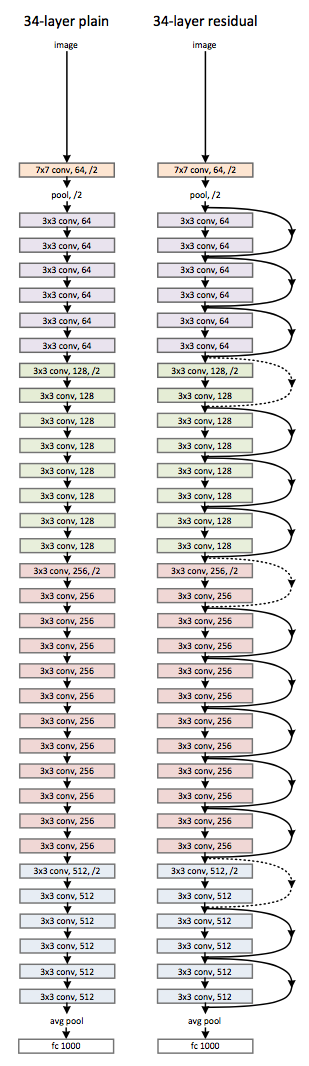
左边的网络是没有添加残差层的网络,作者称它为 plain network,意思就是这个网络很「平」(每次看到这个名字我总是会浮出一些邪恶的想法~囧~)。右边的则是一个完整的深度残差网络,它其实就是由前文所说的小的网络结构组成的,虚线表示要对 \(x\) 的维度进行扩增。作者在两个网络中都加了 Batch Normalization(具体加在卷积层之后,激活层之前),我想目的大概是要在之后的实验中凸显 residual learning 优于 BN 的效果吧。
下面分析一下 identity mapping 对残差网络所起的作用,通过这个最简单的映射来了解 residual learning 不同于一般网络的地方。
首先,给出最通用的网络结构:
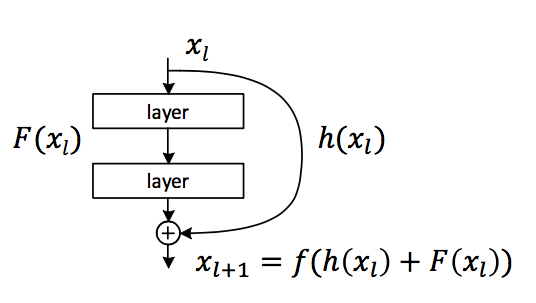
这里其实就是将之前的 \(x\) 换成 \(h(x)\),将最后的 ReLu 换成 \(f(x)\)。因为事实上,\(h(x)\) 和 \(f(x)\) 的形式是很自由的,\(h(x)\) 可以是 \(x\)、\(2x\)、\(x^2\),只要能防止梯度消失或爆炸即可。而 \(f(x)\) 也可以是其他各种激活函数。
不过,因为我们是要从 identity mapping 着手,所以这里还是令 \(h(x)=x\),\(f(x)=x\):
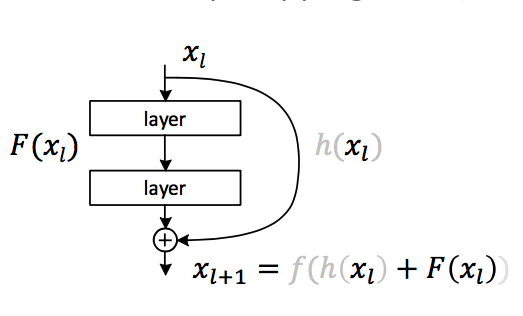
然后,我们用类推出:
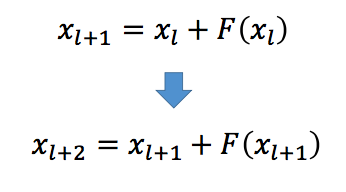
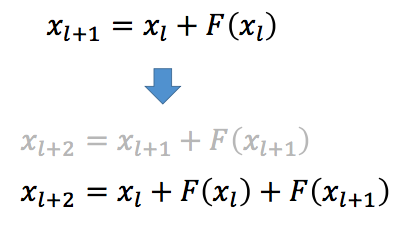
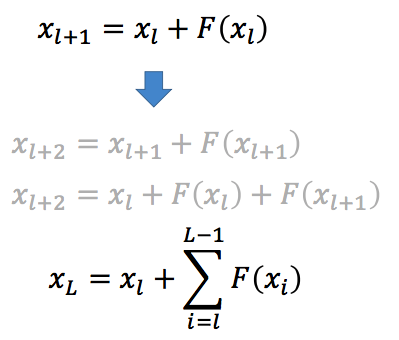
到了这一步,可以发现,在 identity mapping 中,残差网络的输出其实就是在原始输入 \(x_l\) 的基础上,加上后面的一堆「残差」。如果对其求导,则可以得出:
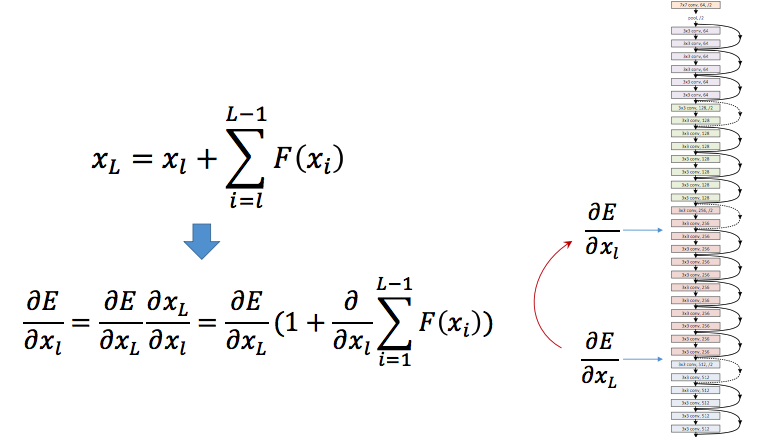
我们发现,导数的形式也很类似,也是最后一层的导数加上前面的一堆「残差」导数,而这一步是残差网络中梯度不容易消失的原因。
作者经过对比实验发现,identity mapping 的效果要好于其他的 mapping,具体的实验细节请参考 tutorial 和后续的一篇论文 Identity Mappings in Deep Residual Networks。换句话说,使用 residual network 时,最好用上 identity mapping。
论文中的实验
实验部分,我只讲一下 ImageNet 的结果。
作者分别用 18 层和 34 层的网络做了两组对比实验(两组网络除了残差外,其他结构相同,并且都加了 BN 层。在对 \(x\) 升维时,直接使用 0 进行 padding,换句话说,残差网络的参数和 plain 的一样。34 层的网络见上一部分的说明),并分析了它们在 ImageNet 训练集上的误差下降情况:
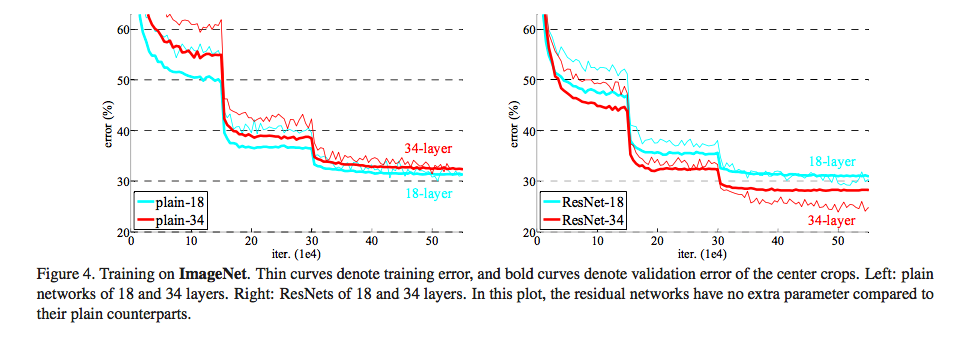
上图中,左图是 plain 网络,右图是 ResNet。注意,训练刚开始的时候,ResNet 的误差下降的速度比 plain 网络要快,也就是说,残差网络的训练速度快于 plain 网络。对于 18 层的网络而言,两者最终的准确率持平,但对于 34 层的网络,使用残差的结果要好于一般的网络。另外,我们再看看验证集上的情况:
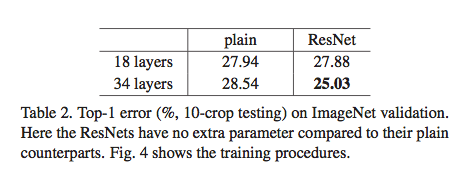
这个结果表明,当网络层数不多时,plain 网络和残差网络除了训练速度不一样外,对最终的结果影响不大。但如果层数比较深,残差网络可以提升准确率。作者在这里提出一个问题:既然我们已经在网络中加了 BN,那导致 plain 网络准确率降不下来的原因应该不会是梯度消失。但又会是其他什么原因呢?作者在论文中称这种问题为 degradation problem,即退化问题。它指的是随着网络层数增加,在梯度没有消失的情况下导致的网络训练缓慢或训练停止的问题。当然啦,按照我自己的理解和猜测,就如这篇文章开篇所讲的那样,梯度消失是由两个方面导致,而 BN 只是将数据从激活函数的收敛区调整到梯度更大的区域,但导数相乘后的累积效应仍然会使梯度变小,所以才导致这里所说的退化问题。不过具体的原因,还有待进一步研究。