在神经网络的训练过程中,总会遇到一个很蛋疼的问题:梯度消失/爆炸。关于这个问题的根源,我在上一篇文章的读书笔记里也稍微提了一下。原因之一在于我们的输入数据(网络中任意层的输入)分布在激活函数收敛的区域,拿 sigmoid 函数举例:
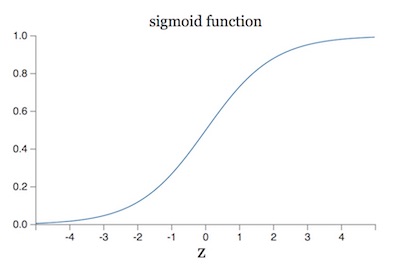
如果数据分布在 [-4, 4] 这个区间两侧,sigmoid 函数的导数就接近于 0,这样一来,BP 算法得到的梯度也就消失了。
之前的笔记虽然找到了原因,但并没有提出解决办法。最近在实战中遇到这个问题后,束手无策之际,在网上找到了这篇论文 Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift。原来早在 2015 年就有人提出了解决方案,而且基本已经成为神经网络的组成部分之一了。本文仅仅是对这篇论文做一些梳理,并总结一些我个人的理解。论文中还有很多不解的地方,因此总结的过程中难免存在错误,还请发现的同学指正☺️
什么是 Batch Normalization
在开始正文之前,不得不先泼一盆冷水:这篇论文虽然解决了梯度消失的一个痛点,但并没有办法根治问题。在实际操作中,我发现用了 Batch Normalization 后,训练的速度确实能得到很大的提升,但也存在完全不起作用的情况。那为什么还要学这篇论文呢?一来,文章的思想很有借鉴意义;二来,虽然方法未必奏效,但用了之后也不会产生什么副作用,况且万一它就奏效了呢;第三,在其他解决梯度消失的文章里面,都会用到这篇论文的方法。所以,不管怎样,在深度学习的优化道路上,这篇论文都是绕过不去的。
为了方便,下面统一用 BN 指代 Batch Normalization。
BN 解决了一个很大的「困扰」,也就是论文中提到的 Internal Covariate Shift。关于什么是 Internal Covariate Shift,我没有读过相关的论文,因此认识也不深。简单理解,就是文章开篇讲的,数据分布在激活函数的收敛区的问题。要「修正」这个问题,一个很自然的想法就是把输入的数据强行掰到中间梯度很大的区域。其实,这种想法我们在数据预处理阶段就用过了,即数据归一化。归一化数据的方式有很多,比如:白化 (whiten) 等。但最简单也最常用的方法是:\(\frac{x - \mu}{\sigma}\),其中 \(\mu\) 是平均数,\(\sigma\) 是标准差。虽然这种方法可以让网络的输入层避免梯度消失的问题,但中间层的数据分布依然不可控。因此,BN 的想法就是,让网络中间每一层的数据都归一化。
比如,我们在数据流向中间任意一层网络的激活函数之前,先做一遍归一化: \[ \hat x^{(k)} \leftarrow \frac{x_i^{(k)} -\mu_{\beta}^{(k)}}{\sqrt{\sigma_{\beta}^{(k)^2}+\epsilon}} \tag{1} \] 其中,\(x_i^{(k)}\) 表示第 k 层网络的输入,\(\mu_{\beta}\) 表示第 k 层所有输入的均值,\(\sigma_{\beta}\) 表示第 k 层所有输入的标准差,\(\epsilon\) 是为了防止除数为 0 而添加的数值,一般取 0.001 即可。
BN 算法
训练阶段
上面我们介绍了 BN 算法的大概思路。不过要注意一个问题,对于神经网络而言,中间每一层的输出结果都是有意义的(比如可能抽取了一些图像特征之类的),如果我们擅自改变中间的数据分布,势必会影响到之后的网络层的结果,换言之,可能改变了网络原有的特征表达能力。因此,我们需要一些额外的措施来弥补这里的损失。
为了恢复网络的表达能力,作者在对数据归一化后,又进行了「还原」操作,这一步应该是整个 BN 算法的精髓。前面提到,归一化就是减去均值同时除以标准差,那还原的公式就变成: \[ x_i^{(k)}=\hat x^{(k)} \sqrt{\sigma_{\beta}^2+\epsilon}+\mu_{\beta}^{(k)} \tag{2} \] 即先对 \(\hat x^{(k)}\) 的尺寸进行缩放,然后平移 \(\mu_{\beta}^{(k)}\) 单位。
不过,如果只是这样直接还原的话,那之前的归一化操作就没有意义了,因此作者兵行险招,引入两个参数:用 \(\gamma^{(k)}\) 表示缩放因子,用 \(\beta^{(k)}\) 表示平移距离。然后将之前的还原公式替换成: \[ y_i^{(k)} \leftarrow \gamma^{(k)} \hat x_i^{(k)}+\beta^{(k)} \tag{3} \] 一开始看到这一步一直很纳闷,这不是换汤不换药吗?不过,这个公式跟之前那个公式有一点不同,那就是缩放的因子和平移的距离在这里不再是固定的,而是两个参数(当然是每一层都会对应两个参数)。这两个参数是可以当作网络的参数进行训练的,相当于我们在原先网络的每个激活函数前又加入一个 BN 层来预处理数据。将它们统一进网络后,就跟其他参数一样,可以通过 BP 进行梯度下降了。在初始化的时候,我们将 \(\gamma\) 初始化为 1.0,将 \(\beta\) 初始化为 0,那么在网络开始训练时,这两个参数对「还原」来说是不起作用的。即刚开始训练的时候,中间每层网络的数据都会经过归一化,从而避免激活函数导数为 0 的问题。随着网络逐渐优化,\(\gamma\) 和 \(\beta\) 会逐渐得到训练,因此中间层的「还原」力度会越来越明显。按照作者的意思(其实是我对论文的理解),当网络优化到一定程度时,\(\gamma\) 和 \(\beta\) 可以还原出原来的数值,这样就可以保证网络对特征的表达能力不会受影响,而此时网络也基本训练完毕了,因此即使梯度消失也就无关紧要了。
不过,我之所以认为这是兵行险招,是因为我不太确定这两个参数是否真能还原回原来的数值。论文中并没有很好的证明,因此这一步我目前还不是很理解。
BN 的算法流程(简单起见去掉符号 (k)):

这里面的 \(x_i\) 并不是网络的训练样本,而是指原网络中任意一个隐藏层的激活函数的输入,当然这些输入也是靠训练样本在网络中前向传播得来的。加了 BN 层后,激活函数的输入就替换为 \(y_i\)。
注意到,网络是针对一个 Batch 进行训练的,中间的平均值 \(\mu_\beta\) 和标准差 \(\sigma_\beta\) 也是针对这个 Batch 计算的,这也是算法名称的由来。
由于我们把 BP 当作是网络中的一个隐藏层,在梯度下降时,可以用 BP 算法求出 \(\gamma\) 和 \(\beta\) 的导数:
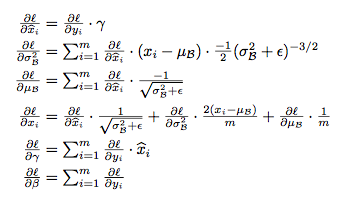
然后把它们也当作网络的参数进行训练即可。
预测阶段
预测阶段不同于训练的地方在于,我们没法通过 Batch 计算出 \(\mu_\beta\) 和 \(\sigma_\beta\) 的值。于是作者用所有训练样本的均值和方差来进行估算。具体做法可以用下面两个式子概括: \[ E[x] \leftarrow E_\beta [\mu_\beta] \tag{4} \]
\[ Var[x] \leftarrow \frac{m}{m-1}E_\beta [{\sigma_\beta} ^2] \tag{5} \]
这里的 \(\mu_\beta\) 和 \(\sigma_\beta\) 指的是某个 mini-batch 样本的均值和标准差。也就是说,作者是在每个 batch 的均值和标准差的基础上,再求出整体的均值和标准差。要注意的是,在求标准差的时候,用了无偏估计 \(\frac{m}{m-1}\)。
不过在预测阶段,其实我们不需要再做归一化加快训练了,所以理论上是可以把 BN 层去掉的。但由于训练时已经将 BN 层和其他的网络层当作一个整体了,直接去掉又会出问题。因此,作者用了一点 trick,他把 BN 中原来归一化的操作去掉,并在「还原」那一步里加入一些措施来抵消「还原」。具体来讲,就是将原来 BN 层的操作替换为: \[ y=\frac{\gamma}{\sqrt{Var[x]+\epsilon}}x+(\beta - \frac{\gamma E[x]}{\sqrt{Var[x]+\epsilon}}) \tag{6} \] 在分析这个式子之前,我们先回顾一下公式 (3)。在公式 (3) 里面,\(y=\gamma x+\beta\),这一步是为了将归一化后的 \(x\) 还原,因此,在作者的想象中,\(\gamma\) 和 \(\beta\) 代表的真实含义其实是样本的标准差和均值,尽管它们也是训练出来的,但作者的想法应该是:它们最终会被优化成接近总样本的标准差和均值。按照这个假设,在公式 (6) 中,\(\frac{\gamma}{\sqrt{Var[x]+\epsilon}}\) 其实就抵消掉了,后面那个偏移量也同理抵消了,所以公式 (6) 本质上就是:\(y=x\)。相当于预测的时候,BN 层不起任何作用。
BN 算法总体流程:

这个算法流程图中的细节在前面都做了详细的解释(当然是按照我自己的理解),所以这里就不展开讲了。
关于代码实现,由于我平时只用 tensorflow,所以参考的实现代码也是基于 tensorflow 的,具体可以参考莫烦Python的教程。
另外,上面的介绍都是针对一般的全联接网络的,具体对于 CNN 或者 RNN 这些网络结构,BN 算法需要做一些修改,鉴于目前我还没有深入学习,因此也就不继续深入讲了,有兴趣的读者还请参考其他资料。
总结
总的来说,BN 其实就是将数据的分布由原来激活函数的收敛区调整到梯度较大的区域,类似于数据的归一化处理,不过为了保持原来网络的特征表达能力,引入一些措施将调整后的数据又还原回去。
但要注意的一点是,由于 BN 只关注于激活函数收敛导致的梯度消失问题,因此,在实际使用中,梯度仍然可能消失(比如:链式求导中,导数的累乘效应可能也会导致梯度消失,具体可以看之前的读书笔记)。在之后的文章中,我将介绍另一种解决梯度消失的方法——深度残差学习 (deep residual learning),这种方法效果上比 BN 更好。
================ UPDATE 2018.3.15 ================
这篇文章刚开始写完时一直在思考一个问题:BN 提出来的时候,ReLu 函数已经大行其道了,而 ReLu 不存在 sigmoid 函数梯度消失的问题,那 BN 不是没什么卵用吗?
今天看了李宏毅教授的视频,发现 BN 其实是要解决另一个更严重的问题,而顺带把函数梯度消失的问题解决了,所以,我上面扯了这么多,居然一直没抓住重点~囧~
BN 其实是要解决 Internal Covariate Shift,没错,这几个关键词就在论文题目里,居然给我省略了。。。这个问题我没有追根溯源去寻找其他文献,但李教授用了一张图让我明白了是怎么回事:
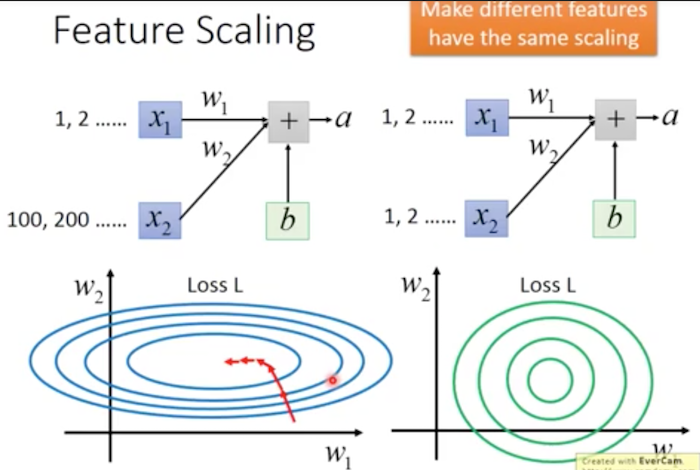
这张图里,同一个特征的两个维度上 \(x_1\)、\(x_2\) 的值的范围是不一样的,这种差别导致训练的时候会非常的缓慢,除非我们针对不同的维度设置不同的学习率,但这是很难办到的。其实,熟悉 Andrew NG 机器学习入门课的人也应该会回忆起 NG 提到的这个问题:
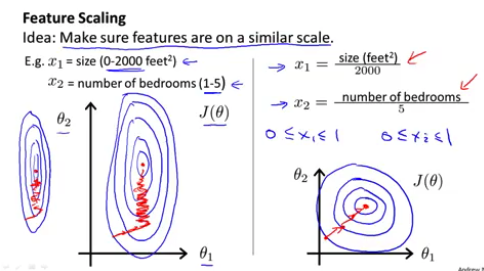
这个问题和李教授图里的内容是一样的,当时 NG 是提到用 feature scaling 的方法解决它。
BN 其实就是在做 feature scaling,而且它的目的也是为了在训练的时候避免这种 Internal Covariate Shift 的问题,只是刚好也解决了 sigmoid 函数梯度消失的问题。