(本文是根据 neuralnetworksanddeeplearning 这本书的第二章How the backpropagation algorithm works整理而成的读书笔记,根据个人口味做了删减)
在上一章的学习中,我们介绍了神经网络可以用梯度下降法来训练,但梯度的计算方法却没有给出。在本章中,我们将学习一种计算神经网络梯度的方法——后向传播算法(backpropagation)。
backpropagation 算法起源于上个世纪 70 年代,但一直到 Hinton 等人在 1986 年发表的这篇著名论文后才开始受到关注。BP 算法使得神经网络的训练速度快速提升,因此它是学习神经网络的重中之重。
热身:一种基于矩阵的快速计算神经网络输出的方法
在开始讨论 BP 算法之前,我们先回顾一种基于矩阵形式的计算神经网络输出的方法。
首先,引入几个符号表示。
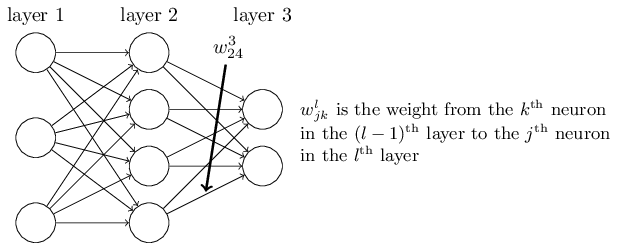
假设 \(w_{jk}^{l}\) 表示从第 l-1 层的第 k 个神经元到第 l 层的第 j 个神经元的权值,如下图所示。
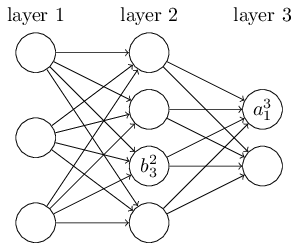
假设 \(b_{j}^{l}\) 表示 l 层第 j 个神经元的偏差,\(a_{j}^{l}\) 表示 l 层第 j 个神经元的激活层,如下图所示:
有了这些标记,第 l 层的第 j 个神经元的激活层 \(a_{j}^{l}\) 就可以和 l-1 层的激活层关联起来: \[ a_{j}^l = \sigma(\sum_{k}{w_{jk}^{l}a_{k}^{l-1}+b_{j}^{l}}) \tag{23} \] 其中,\(\sigma()\) 是一个激活函数,例如 sigmoid 函数之类的。
现在,为了方便书写,我们为每一层定义一个权值矩阵 \(W^l\),矩阵的每个元素对应上面提到的 \(w_{jk}^{l}\)。类似地,我们为每一层定义一个偏差向量 \(b^l\) 以及一个激活层向量 \(a^l\)。
然后,我们将公式 (23) 表示成矩阵的形式: \[ a^l=\sigma(W^la^{l-1}+b^l) \tag{25} \] 注意,这里我们对 \(\sigma()\) 函数做了点延伸,当输入参数是向量时,\(\sigma()\) 会逐个作用到向量的每个元素上(elementwise)。
在 (25) 式中,有时为了书写的方便,我们会用 \(z^l\) 来表示 \(W^la^{l-1}+b^l\)。下文中,\(z^l\) 将会频繁出现。
损失函数的两个前提假设
BP 算法的目标是要计算偏导数 \(\partial C\)/\(\partial w\) 和 \(\partial C\)/\(\partial b\),要让 BP 算法起作用,我们需要两个前提假设:
- 损失函数可以表示成 \(C=\frac{1}{n}\sum_{x}{C_x}\),其中 \(C_x\) 是每个训练样本 x 的损失函数。
- 损失函数用神经网络的输出作为函数的输入:
BP 算法背后的四个基本公式
BP 算法本质上是为了计算出 \(\partial C\) / \(\partial w_{jk}^{l}\) 和 \(\partial C\) / \(\partial b_{j}^{l}\)。为了计算这两个导数,我们引入一个中间变量 \(\delta_{j}^{l}\),这个中间变量表示第 l 层第 j 个神经元的误差。BP 算法会计算出这个误差,然后用它来计算\(\partial C\) / \(\partial w_{jk}^{l}\) 和 \(\partial C\) / \(\partial b_{j}^{l}\)。
\(\delta_{j}^{l}\) 被定义为: \[ \delta _{j}^{l}=\frac{\partial C}{\partial z_{j}^{l}} \tag{29} \] 这个定义来源于这样一个事实:损失函数 \(C\) 可以看作是关于 \(z\) 的函数,而 \(z\) 是 \(W\) 和 \(b\) 的线性组合(考虑到损失函数的两个前提假设,\(C\) 是关于网络输出 \(a\) 的函数,而 \(a\) 又是 \(z\) 的函数,所以 \(C\) 也可以看作是 \(z\) 的函数)。其实,我们也可以将它定义为:\(\delta_{j}^{l}=\frac{\partial C}{\partial a_{j}^{l}}\)(\(a\) 是神经网络某一层的输出),但这样会导致之后的计算十分复杂,所以,我们还是保留原先的定义。
BP 算法基于 4 个基本公式,这些公式会告诉我们如何计算 \(\delta^{l}\) 和损失函数的梯度。
输出层误差 \(\delta^{L}\)的计算公式
\[ \delta_{j}^{L}=\frac{\partial C}{\partial z_{j}^{L}}=\frac{\partial C}{\partial a_{j}^{L}}\sigma'(z_{j}^{L}) \tag{BP1} \]
这个公式是最直接的,只需要知道 \(a^{L}=\sigma(z^{L})\),然后根据链式法则即可得到。
为了更好地运用矩阵运算,我们改变一下上面式子的形式: \[ \delta^{L}=\nabla_a C \odot \sigma'(z^L). \tag{BP1a} \] 其中,\(\odot\) 表示 elementwise 运算,而 \(\nabla_a C\) 可以看作是 \(\partial C / \partial a_{j}^{L}\) 组成的向量。
举个例子,假设 \(C=\frac{1}{2}\sum_{j}{(y_j - a_{j}^{L})}^2\),则 \(\partial C / \partial a_{j}^{L}=\begin{bmatrix} \partial C / \partial a_0^l \\ \partial C / \partial a_1^l \\ \vdots \\ \partial C / \partial a_n^l \end{bmatrix}=(a_{j}^{L}-y_j)=\begin{bmatrix} a_0^l-y_0 \\ a_1^l-y_1 \\ \vdots \\ a_n^l-y_l \end{bmatrix}\),那么公式(BP1)可以表示成:\(\delta^{L}=(a_{L}-y) \odot \sigma'(z^L)\)。
\(\delta^L\)与\(\delta^{L+1}\)的计算公式
\[ \delta^L=((w^{l+1})^T\delta^{l+1}) \odot \sigma'(z^l) \tag{BP2} \]
前面公式 (BP1) 可以让我们计算出最后输出层 \(\delta^L\) 的值,而 (BP2) 这个公式可以依据最后一层的误差,逐步向前传递计算前面输出层的 \(\delta^L\) 值。
bias 的导数计算公式
\[ \frac{\partial C}{\partial b_j^{l}}=\delta_j^l \tag{BP3} \]
这个公式表明,第 l 层偏差 bias 的导数和第 l 层的误差值相等。
权重 W 的导数计算公式
\[ \frac{\partial C}{\partial w_{jk}^{l}}=a_{k}^{l-1}\delta_{j}^{l} \tag{BP4} \]
同理,这个公式揭露出权重 W 的导数和误差以及网络输出之间的关系。用一种更简洁的方式表示为: \[ \frac{\partial C}{\partial w} = a_{in}\delta_{out} \tag{32} \] 其中,\(a_{in}\) 是权重 \(W\) 的输入,而 \(\delta_{out}\) 是权重 \(W\) 对应的 \(z\) 的误差。用一幅图表示如下:
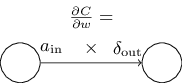
公式 (32) 一个很好的效果是:当 \(a_{in} \approx 0\) 时,梯度公式的值会很小,换句话说,当权重 \(W\) 的输入 \(a_{in}\),也就是上一层激活层的输出接近 0 时,那么这个激活层对网络的影响就变得很小,\(W\) 的学习也会变得很慢。
一些启发(insights)
根据上面四个公式,可以发现,当最后输出层的导数 \(\sigma'(z^L)\) 变的很小时(即网络本身已经接近收敛),权重 \(W\) 和偏差 \(b\) 会逐渐停止学习(因为误差 \(\delta\) 逐渐趋于 0)。
当然,不单单是最后一层会影响学习速度,根据公式 (BP2),当中间层的导数 \(\sigma'(z^l)\) 也开始趋于 0 时,那么上一层的误差 \(\delta^l\) 也会趋于 0,从而导致上一层权重 \(W\) 和偏差 \(b\) 的学习也会开始停止。
总之,当 \(W\) 的输入 \(a\) 变的很小或者输出层 \(\sigma(z^l)\) 收敛时,网络权值的训练将会变得很慢。
需要注意的一点是,这四个公式的推导适用于任何激活函数。因此,我们完全可以用其他函数来取代 \(sigmoid()\)。比如,我们可以设计一个函数 \(\sigma()\),这个函数的导数 \(\sigma'()\) 永远为正,且 \(\sigma()\) 函数值永远不会接近 0,那么就可以避免上面提到的学习停止的问题。
最后,总结一下 BP 的 4 个基本公式:

个人对于误差以及 BP 的理解
根据误差 \(\delta\) 的定义,不难发现,它其实就是损失函数关于参数 \(W\) 和 \(b\) 的间接导数,这一点跟第一章中对梯度的定义是一致的。当 \(\delta\) 越大时,证明网络还远没有收敛,即网络的「误差」还很大,因此需要学习更多,反之,则证明网络的「误差」比较小,学习可以停止了。
网络中每一层的误差都需要借助前一层的误差进行计算,这个过程其实是一个导数的叠加过程,可以感性地认为,整个神经网络其实是由一个个函数复合在一起形成的,因此,导数的计算其实就是链式法则的不断应用,前面层神经元的导数需要后面层神经元导数不断叠加,这个过程就构成了后向传播算法。
公式证明
BP1
公式 (BP1) 的证明是十分简单的,不过需要习惯向量或矩阵的 elementwise 的求导形式。
我们假设 \(C=f(\sigma(z^L))=f(\sigma(z_0^L), \sigma(z_1^L), \cdots, \sigma(z_n^L))\),根据定义 \(\delta_j^L=\frac{\partial C}{\partial z_j^L}\),由于 \(z_j^L\) 只跟 \(a_j^L\) 相关,于是我们用链式法则可以得到(可以画个网络图帮助理解): \[ \delta_j^L=\frac{\partial f}{\partial \sigma(z_j^L)}\frac{\partial \sigma(z_j^L)}{\partial z_j^L}=\frac{\partial C}{\partial a_j^L}\frac{\partial a_j^L}{\partial z_j^L} \tag{38} \] 其中,\(a_j^L=\sigma(z_j^L)\),我们也可以将它表示成另一种形式: \[ \delta_j^L=\frac{\partial C}{\partial a_j^L}\sigma'(z_j^L) \tag{39} \] 上式就是 BP1 的形式了。
BP2
BP2 需要用到后一层计算出来的 \(\delta^{l+1}\),因此,我们先根据 BP1 得出:\(\delta_k^{l+1}=\frac{\partial C}{\partial z_k^{l+1}}\)。
由 \(\delta_k^{l}=\frac{\partial C}{\partial z_k^l}\) 和 \(C=f(\sigma(z_0^L), \sigma(z_1^L), \cdots, \sigma(z_n^L))\) 可以得到: \[ \begin{eqnarray} \delta_j^{l} & = & \frac{\partial C}{\partial z_0^{l+1}}\frac{\partial z_0^{l+1}}{\partial z_j^{l}}+\cdots+\frac{\partial C}{\partial z_n^{l+1}}\frac{\partial z_n^{l+1}}{\partial z_j^{l}} \notag \\ & = & \sum_k{\frac{\partial C}{\partial z_k^{l+1}}\frac{\partial z_k^{l+1}}{\partial z_j^j}} \notag \\ & = & \sum_k \delta_k^{l+1}\frac{\partial z_k^{l+1}}{\partial z_j^{l}} \tag{42} \end{eqnarray} \]
我们还要进一步找出 \(z_k^{l+1}\) 和 \(z_k^{l}\) 之间的关系。根据前向传播,可以得到: \[ z_k^{l+1}=\sum_j{w_{kj}^{l+1}a_j^l+b_k^{l+1}}=\sum_j{w_{kj}^{l+1}\sigma(z_j^l)+b_k^{l+1}} \tag{43} \] 进而可以得到: \[ \frac{\partial z_k^{l+1}}{\partial z_j^l}=w_{kj}^{l+1}\sigma'(z_j^l) \tag{44} \]
将式 (44) 代入 (42) 得: \[ \delta_j^l=\sum_k{w_{kj}^{l+1}\sigma'(z_j^l)\delta_k^{l+1}}=\sigma'(z_j^l)\sum_k{w_{kj}^{l+1}\delta_k^{l+1}} \tag{45} \] 表示成矩阵的形式就是: \[ \delta^L=((w^{l+1})^T\delta^{l+1}) \odot \sigma'(z^l) \] 即 BP2 的公式,注意矩阵的转置运算。
BP3
\[ z_j^l=\sum_k{W_{jk}^l a_k^{l-1}}+b_j^l \]
\[ \frac{\partial z_j^l}{\partial b_j^l}=1 \]
\[ \frac{\partial C}{\partial b_j^l}=\frac{\partial C}{\partial z_j^l}\frac{\partial z_j^l}{\partial b_j^l}=\frac{\partial C}{\partial z_j^l}=\delta_j^l \]
BP4
证明过程同 BP3: \[ z_j^l=\sum_k{W_{jk}^l a_k^{l-1}}+b_j^l \]
\[ \frac{\partial z_j^l}{\partial W_{jk}^l}=a_k^{l-1} \]
\[ \frac{\partial C}{\partial W_{jk}^l}=\frac{\partial C}{\partial z_j^l}\frac{\partial z_j^l}{\partial W_{jk}^l}=\frac{\partial C}{\partial z_j^l}a_k^{l-1}=\delta_j^la_k^{l-1} \]
后向传播算法(BP)
- Input x: Set the corresponding activation \(a^1\) for the input layer.
- Feedforward: For each l = 2, 3, …, L compute \(z^l=w^la^{l-1}+b^l\) and \(a^l=\sigma(z^l)\).
- Output error \(\delta^L\): Compute the vector \(\delta^L=\nabla_a C \odot \sigma'(z^L)\).
- Backpropagate the error: For each l = L-1, L-2, …, 2 compute \(\delta^l=((W^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l)\).
- Output: The gradient of the cost function is given by \(\frac{\partial C}{\partial w_{jk}^l}=a_k^{l-1}\delta_j^{l}\) and \(\frac{\partial C}{\partial b_j^l}=\delta_j^l\).
以上算法是针对一个训练样本进行的,实际操作中,通常是用随机梯度下降算法,用几个样本进行训练,因此我们将算法略微修改如下:
- Input a set of training examples
- For each training example x: Set the corresponding input activation \(a^{x, 1}\), and perform the following steps:
- Feedforward: For each l = 2, 3, …, L compute \(z^{x, l}=w^la^{x, l-1}+b^l\) and \(a^{x, l}=\sigma(z^{x,l})\).
- Output error \(\delta^{x, L}\): Compute the vector \(\delta^{x, L}=\nabla_a C_x \odot \sigma'(z^{x,L})\).
- Backpropagate the error: For each l = L-1, L-2, …, 2 compute \(\delta^{x,l}=((W^{l+1})^T \delta^{x,l+1}) \odot \sigma'(z^{x,l})\).
- Gradient descent: For each l = L, L-1, …, 2 update the weights according to the rule \(W^l \rightarrow W^l-\frac{\eta}{m} \sum_x \delta^{x,l}(a^{x,l-1})^T\), and the biases according to the rule \(b^l \rightarrow b^l - \frac{\eta}{m} \sum_x{\delta^{x,l}}\).