(本文是根据 neuralnetworksanddeeplearning 这本书的第三章Improving the way neural networks learn整理而成的读书笔记,根据个人口味做了删减)
上一章中,我们领略了神经网络中最重要的算法:后向传播算法(BP)。它使得神经网络的训练成为可能,是其他高级算法的基础。今天,我们要继续学习其他方法,这些方法使得网络的训练结果更好。
这些方法包括:
- 更好的损失函数:交叉熵(cross-entropy)函数
- 四种正规化方法:L1、L2、dropout以及数据集的人工增广
- 一种更好的初始化权值的方法
- 一系列选择 hyper-parameters 的启发策略
- 其他一些小技巧
交叉熵函数(cross-entropy)
实际生活中,我们都会有这样的经验:当遇到错误的时候,往往是我们学到东西最多的时候,而如果我们对自己的错误模糊不清,进步反而会变慢。
同样地,我们希望神经网络能够从错误中更快地学习。那实际情况是怎样的呢?来看一个简单的例子。
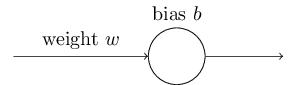
这个例子只包含一个神经元,并且只有一个输入。我们会训练这个神经元,使得:当输入为 1 时,输出为 0。我们将权重和偏差分别初始化为 0.6 和 0.9。当输入为 1 时,网络输出为 0.82 (\(\frac{1}{1+e^{-1.5}} \approx 0.82\))。我们采用平方差函数来训练网络,并将学习率设为 0.15。
这个网络其实已经退化成一个线性回归模型。下面用一个动画来演示网络的训练过程:
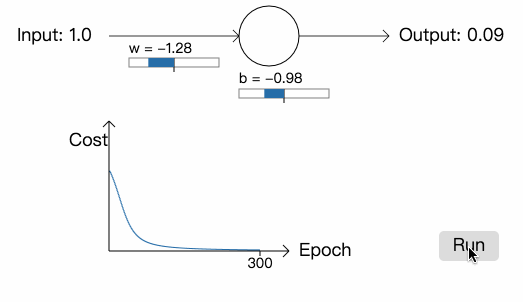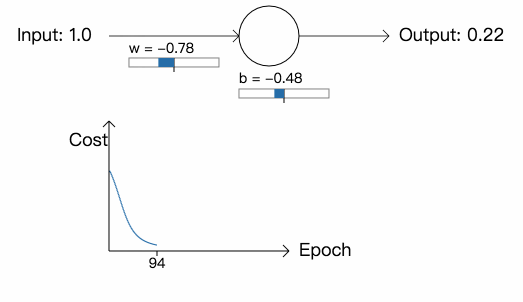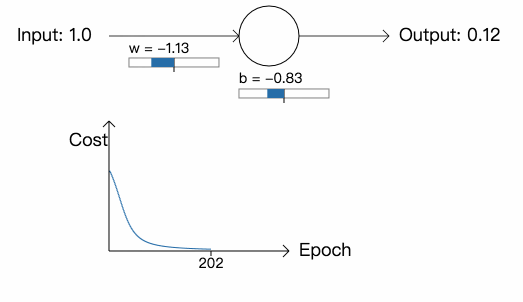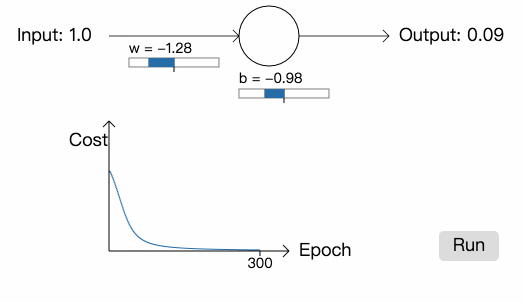
从中我们可以看到,神经元快速地学习参数,最终输出 0.09 (已经很接近 0 了)。现在,我们将参数和偏差初始化为 2.0,网络的初始输出为 0.98 (跟我们想要的结果相差甚远),学习率依然为 0.15。看看这一次网络会如何学习:
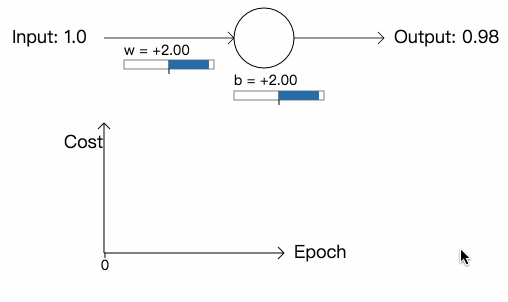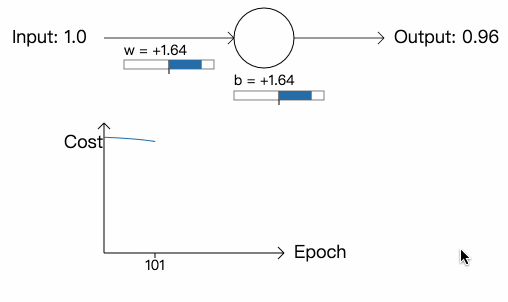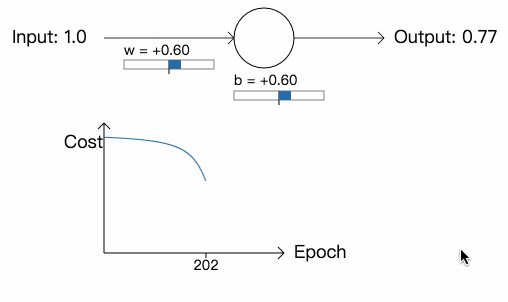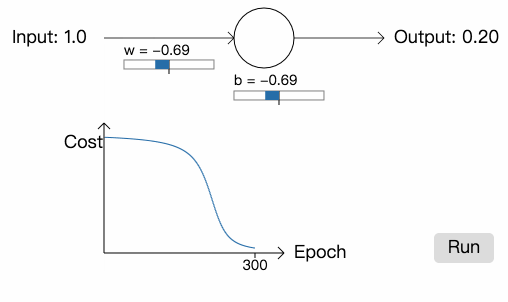
虽然学习率和上次一样,但网络一开始学习的速度却很慢,在最开始的 150 次学习里,参数和偏差几乎没有改变,之后,学习速度突然提高,神经元的输出快速降到接近 0.0。这一点很令人差异,因为当神经元的输出严重错误时,学习的速度反而不是很快。
下面我们需要了解问题发生的根源。神经元在训练的时候,学习速度除了受学习率影响外,还受偏导数 \(\partial C/ \partial w\) 和 \(\partial C / \partial b\) 影响。所以,学习速度很慢,也就是偏导数的值太小。根据 \[ C=\frac{(y-a)^2}{2} \tag{54} \] (其中,\(a=\sigma(z)\),\(z=wx+b\)),我们可以求出(下面两个式子中,已经将 x 和 y 的值替换为 1 和 0): \[ \frac{\partial C}{\partial w} = (a-y)\sigma'(z)x=a\sigma'(z) \tag{55} \]
\[ \frac{\partial C}{\partial b} = (a-y)\sigma'(z)=a\sigma'(z) \tag{56} \]
要想深入理解这两个式子,我们需要回顾一下 sigmoid 函数的内容,如下图:
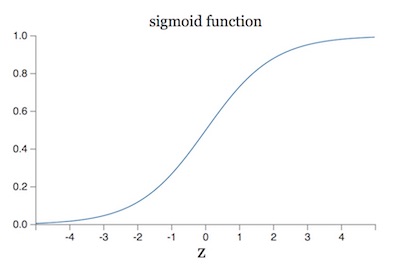
从函数图像我们可以发现,当函数值接近于 1 或 0 时,函数导数趋于 0,从而导致 (55) 和 (56) 两个式子的值趋于 0。这也是为什么神经元一开始的学习速率会那么慢,而中间部分学习速度会突然提升。
引入交叉熵损失函数
要解决学习速度下降的问题,我们需要从两个偏导数上面做文章。要么换一个损失函数,要么更换 \(\sigma\) 函数。这里,我们采用第一种做法,将损失函数更换为交叉熵函数(cross-entropy)。
首先用一个例子来介绍交叉熵函数。
假设我们有如下神经元:
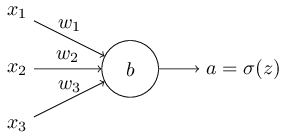
则交叉熵函数被定义为(这里假定 y 是个概率值,在 0~1 之间,这样才能跟 a 相搭): \[ C=-\frac{1}{n}\sum_x{[y \ln a + (1-y) \ln (1-a)]} \tag{57} \] 当然,直觉上看不出这个函数能解决学习速率下降的问题,甚至看不出这可以成为一个损失函数。
我们先解释为什么这个函数可以作为损失函数。首先,这个函数是非负的,即 \(C>0\)(注意 \(a\) 的值在 0~1 之间)。其次,当神经元实际输出跟我们想要的结果接近时,交叉熵函数值会趋近 0。因此,交叉熵满足损失函数的基本条件。
另外,交叉熵解决了学习速率下降的问题。我们将 \(a=\sigma(z)\) 代入 (57) 式,并运用链式法则可以得到(这里的 \(w_j\) 应该特指最后一层的参数,即 \(w_j^L\)): \[ \begin{eqnarray} \frac{\partial C}{\partial w_j} & = & -\frac{1}{n} \sum_x \left( \frac{y }{\sigma(z)} -\frac{(1-y)}{1-\sigma(z)} \right) \frac{\partial \sigma}{\partial w_j} \tag{58}\\ & = & -\frac{1}{n} \sum_x \left( \frac{y}{\sigma(z)} -\frac{(1-y)}{1-\sigma(z)} \right)\sigma'(z) x_j. \tag{59}\end{eqnarray} \] 化简上式并将 \(\sigma(z)=\frac{1}{1+e^{-z}}\) 代入后得到: \[ \frac{\partial C}{\partial w_j}=\frac{1}{n}\sum_x {x_j(\sigma(z)-y)} \tag{61} \] 这个表达式正是我们想要的!它表明,学习速率由 \(\sigma(z)-y\) 控制,也就是说,当误差越大时,学习速率越快。而且避免了 \(\sigma'()\) 导致的学习速率下降的问题。
类似地,我们可以计算出: \[ \frac{\partial C}{\partial b}=\frac{1}{n}\sum_x{(\sigma(z)-y)} \tag{62} \] 现在,我们将交叉熵应用到之前的例子中,看看神经元的训练有什么变化。
首先是权重和偏差的初始值为 0.6 和 0.9 的例子:
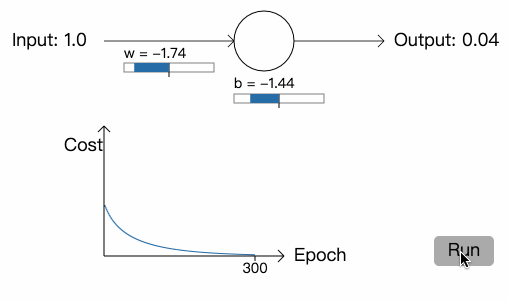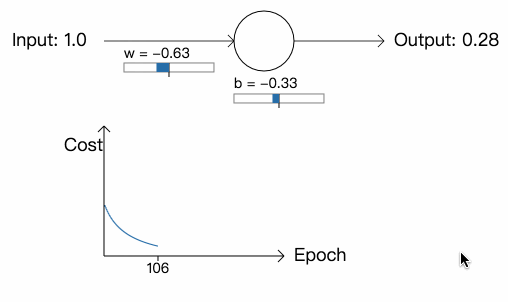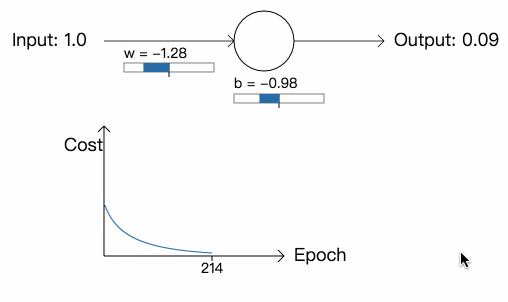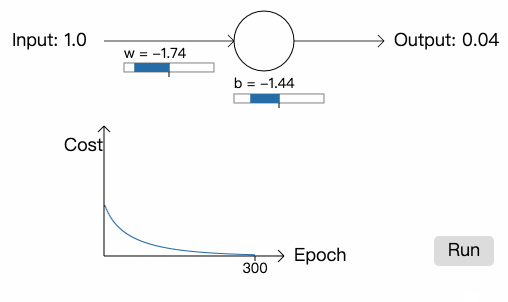
可以看到网络的训练速度近乎完美。
然后是权重和偏差初始值均为 2.0 的例子:
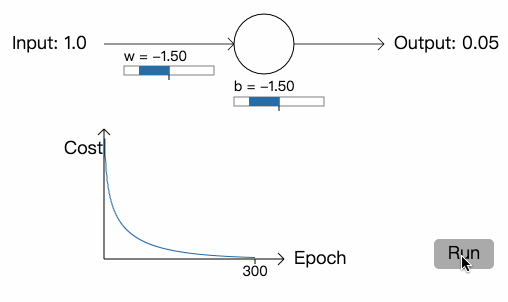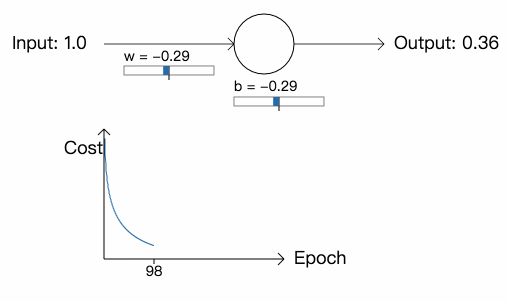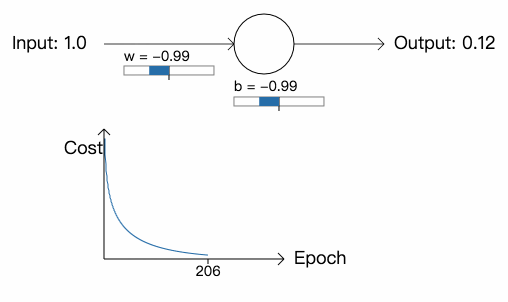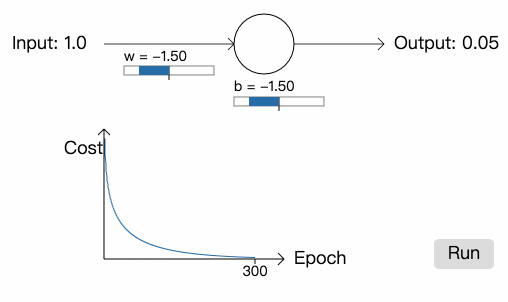
这一次,正如我们期望的那样,神经元学习得非常快。
这两次实验中,采用的学习率是 0.005。事实上,对于不同的损失函数,学习率要作出相应的调整。
上面对交叉熵函数的讨论都只针对一个神经元,其实很容易将它延伸到多层神经元的网络结构。假设 \(y=y_1, y_2, \dots\) 是想要的网络输出,而 \(a_1^L, a_2^L, \dots\) 是网络的实际输出,则 cross-entropy 函数可以定义为: \[ C=-\frac{1}{n}\sum_x \sum_y {[y_j \ln a_j^L + (1-y_j) \ln(1-a_j^L)]} \tag{63} \] 好了,介绍了这么多,那我们什么时候用平方差函数,什么时候用交叉熵呢?作者给出的意见是,交叉熵几乎总是更好的选择,而原因也跟上文提到的一样,平方差函数容易在开始的时候遇到训练速率较慢的问题,而交叉熵则没有这种困扰。当然,这个问题出现的前提是平方差函数中用了 sigmoid 函数。
交叉熵到底是什么,它是怎么来的?
这一节中,我们想知道,第一个吃螃蟹的人是怎么想到交叉熵函数的。
假设我们发现了学习速率下降的根源在于 \(\sigma'(z)\) 函数,我们要如何解决这个问题呢?当然,方法有很多,这里我们考虑这样的思路:是否能找一个新的损失函数,将 \(\sigma'(z)\) 这个项消掉?假如我们希望最终的偏导数满足下面的形式: \[ \frac{\partial C}{\partial w_j}=x_j (a-y) \tag{71} \]
\[ \frac{\partial C}{\partial b}=(a-y) \tag{72} \]
这两个偏导数能使神经网络在误差越大时,训练速度越快。
回忆 BP 的四个公式,可以得到: \[ \frac{\partial C}{\partial b}=\frac{\partial C}{\partial a}\sigma'(z) \tag{73} \] 这里的 \(\sigma()\) 函数采用的是 sigmoid,所以 \(\sigma'(z)=\sigma(z)(1-\sigma(z))=a(1-a)\),将这个式子代入 (73) ,得到: \[ \frac{\partial C}{\partial b}=\frac{\partial C}{\partial a}a(1-a) \] 跟我们最终的目标 (72) 式比较,需要满足: \[ \frac{\partial C}{\partial a}=\frac{a-y}{1(1-a)} \tag{75} \] 对 (75) 进行积分后,便得到: \[ C=-\frac{1}{n}\sum_x{[y\ln a+(1-y)\ln(1-a)]}+constant \tag{77} \] 至此,我们已经推出了交叉熵函数的形式。
当然啦,交叉熵真正的来源是信息论,更具体的介绍超出了本教程的范畴,所以就不再深入了。
Softmax
前一节中,我们重点介绍了交叉熵如何解决训练速度下降的问题,这是从损失函数的角度思考问题。其实,我们还有另一种方法,那就是更换 \(\sigma()\) 函数。这里要简单介绍一个新的 \(\sigma()\) :Softmax。
Softmax 的功能和 sigmoid 类似,只不过前者的函数形式是这样的: \[ a_j^L=\frac{e^{z_j^L}}{\sum_k{e^{z_k^L}}} \tag{78} \] ⚠️分母是所有输出神经元的总和。这意味着,经过 Softmax 函数后,所有神经元的输出会呈现出概率分布的样式。
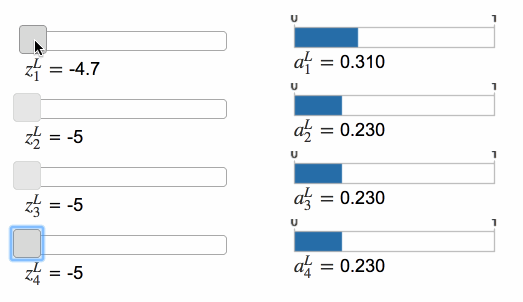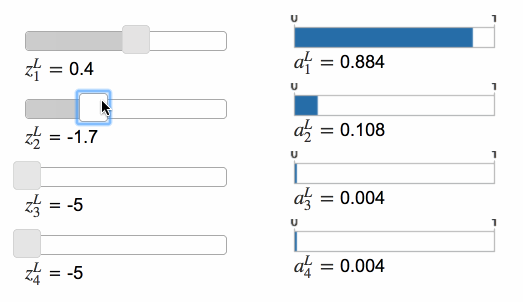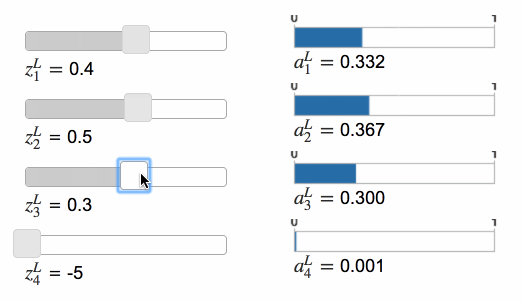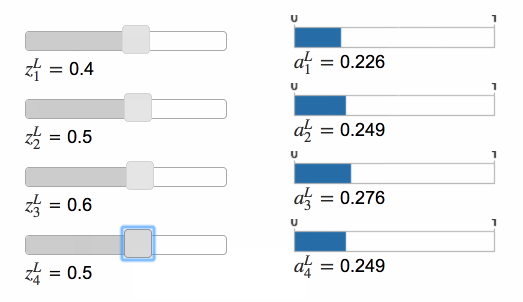
当增大其中一个神经元输出时,其他神经元的输出值会变小,而且变小的总和等于前者增加的值。反之亦然。这是因为所有神经元的输出值总和始终为 1。
另外,Softmax 的输出始终为正值。
Softmax 解决学习速率下降的问题
这一次,我们定义一个 log-likelihood 损失函数,通过它来了解 Softmax 如何缓解 learning slowdown 的问题。
log-likelihood 的函数形式为: \[ C \equiv -\ln a_y^L \tag{80} \] 先解释一下 \(a_y^L\),比方说,在 MNIST 数据集中,我们要判断一张图片属于 10 类中的哪一类,那么,输出结果应该是一个 10 维的向量 \(a^L\),而真实结果则是数字 \(y\),比如 7。那么,\(a_y^L\) 则表示 \(a_7^L\) 这个项对应的概率值有多高。如果概率值(靠近 1)越高,证明猜测结果越正确,那么 \(C\) 的值就越小,反之越大。
有了损失函数后,我们照样求出偏导数: \[ \frac{\partial C}{\partial b_j^L}=a_j^L-y_j \tag{81} \]
\[ \frac{\partial C}{\partial w_{jk}^L}=a_k^{L-1}(a_j^L-y_j) \tag{82} \]
这里不存在类似 sigmoid 导数那样使学习速率下降的情况。
(写到这里的时候,我突然产生一个疑惑:不管是这里的 Softmax,还是的交叉熵,我们都只是对最后一层的导数和偏差求了偏导,但前面层的偏导数却没有计算,怎么能肯定前面层的偏导就不会遇到 \(\sigma'()\) 趋于 0 的问题呢?要知道,根据 BP 算法的公式,误差有这样的传递公式:\(\delta^l\)=\(((W^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l)\),注意,这里依然会出现 \(\sigma'()\),而前面层的权重和偏差的偏导数又是根据这个误差计算的,这样的话,前面层的学习速率下降的问题不还是没解决吗?这个问题先暂时放着,看看之后作者有没有解答。)
写了这么多,我们又要问一个类似的问题:什么时候用 sigmoid 和 cross-entropy,什么时候用 softmax 和 log-likelihood。事实上,大部分情况下这两个选择都能带来不错的结果,当然,如果想要输出结果呈现概率分布的话,Softmax 无疑会更好。