过去一直没有做年终总结的习惯，因为我之前的习惯是脚踏实地的做完眼前的小事情，也从来没给自己确立过什么目标，因此年终的时候也就平平无奇，既没有那种水到渠成的坦然，也没有那种吹尽狂沙始到金的欣慰。但 2018 确实给我带来了不少成长，也是我这些年来过得最不淡定的一年，有些不淡定可能会一直延续到 2019。在我真正能做到拨云见日之前，希望这篇文章能为今后的决定提供一些勇气和思路。

这两天导师让我到桂林参加一个学术会议，不过由于会议太水，加之我出发得太晚，等到桂林的时候，会议差不多结束了。我想我也不能无功而返，就趁着公费出差的机会，在这个号称「山水甲天下」的城市，以一个单身狗该有的心态逛了一圈。

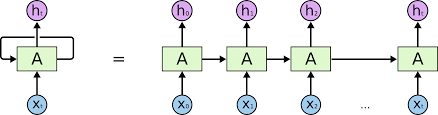
曾经，为了处理一些序列相关的数据，我稍微了解了一点递归网络 (RNN) 的东西。由于当时只会 tensorflow，就从官网上找了一些 tensorflow 相关的 demo，中间陆陆续续折腾了两个多星期，才对 squence to sequence，sequence classification 这些常见的模型和代码有了一些肤浅的认识。虽然只是多了时间这个维度，但 RNN 相关的东西，不仅是模型搭建上，在数据处理方面的繁琐程度也比 CNN 要高一个 level。另外，我也是从那个时候开始对 tensorflow 产生抵触心理，在 tf 中，你知道 RNN 有几种写法吗？你知道 dynamic_rnn 和 static_rnn 有什么区别吗？各种纷繁复杂的概念无疑加大了初学者的门槛。后来我花了一两天的时间转向 pytorch 后，感觉整个世界瞬间清净了 (当然了，学 tf 的好处就是转其他框架的时候非常快，但从其他框架转 tf 却可能生不如死)。pytorch 在模型搭建和数据处理方面都非常好上手，比起 tf 而言，代码写起来更加整洁干净，而且开发人员更容易理解代码的运作流程。不过，在 RNN 这个问题上，新手还是容易犯嘀咕。趁着这一周刚刚摸清了 pytorch 搭建 RNN 的套路，我准备记录一下用 pytorch 搭建 RNN 的基本流程，以及数据处理方面要注意的问题，希望后来的同学们少流点血泪…

至于 tf 怎么写 RNN，之后有闲再补上 (我现在是真的不想回去碰那颗烫手的山芋😩)

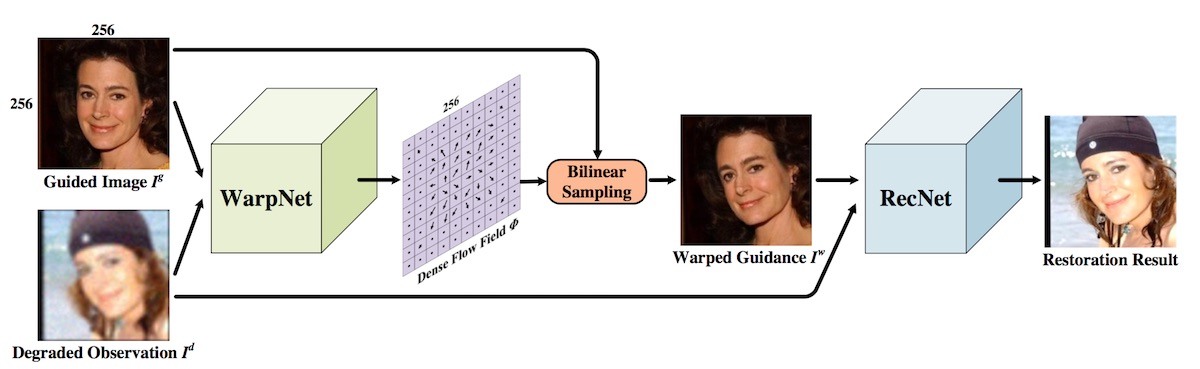
这篇论文主要是讲人脸修复的，所谓人脸修复，其实就是将低清的，或者经过压缩等操作的人脸图像进行高清复原。这可以近似为针对人脸的图像修复工作。在图像修复中，我们都会假设退化的图像是高清图像经过某种函数映射后得到的（比如，由高清图像得到一张模糊的图像可能是使用了高斯模糊核），因此，图像修复的本质就是把这个函数映射找出来。由于神经网络可以近似任意函数，因此在深度学习时代，图像修复已经是一个被解决得比较好的问题了。比如，在图像去噪或者超分任务中，U-Net、FCN 之类的网络结构已经成为标配了。

不过，针对人脸的图像修复则是一个更为严苛的任务。原因主要是以下两点：

1. 对于一般的图像，大家可能不会太在意细节恢复得好还是差，但对于人脸来说，由于这是人类最熟悉的部分，因此人脸中的很多细节，如一些皱纹、酒窝等都需要恢复出来才能让人满意，因此，这是一个粒度更细的图像修复任务。
2. 另外，通常的图像修复都是针对一种退化场景设计的，比如，在去噪任务中，可能就只是针对某种或某几种噪声而言，而不考虑图像模糊等其他因素，因此任务相对简单。但如果退化的种类太多，退化函数本身可能会非常复杂，即使神经网络也未必能近似出来。正如标题中 blind 所言，退化函数的类型、数量我们是无法事先获悉的。事实上，论文考虑了 jpeg 压缩、高斯模糊、高斯噪声、图片放缩等退化方式，并且对每种方式进行随机组合，因此退化函数是非常复杂的。

这天，老板跟你说，希望能在手机上跑深度神经网络，并且准确率要和 VGG、GoogleNet 差不多。

接到这个任务后你有点懵逼，这些网络别说计算量大，就连网络参数也要 100MB 的空间才存得下，放在手机上跑？开玩笑呗。

老板又说，怎么实现是你的事，我要的只是这个功能。

你默默地点了点头。

我在很久以前的一篇短文提过一丢丢 boosting，今天翻了下统计学习方法，打算记录一点干货的东西。这篇博文会简单介绍一下 「Adaboost」，并总结一下 Adaboost 方法背后的套路：前向分步加法模型。

这篇文章想简单讲讲 KMP 算法的内容。

KMP 算法

KMP 算法由 Knuth–Morris–Pratt 三个人共同提出，它的目的是判断字符串 A 中是否包含另一个字符串 B（如：判断 abababaababacb 中是否包含 ababacb）。

题目

原题：Given a binary tree, determine if it is a valid binary search tree (BST).

Assume a BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• Both the left and right subtrees must also be binary search trees.

Example 1:

1
2
3

  2
 / \
1   3

Binary tree [2,1,3], return true.

Example 2:

1
2
3

  1
 / \
2   3

Binary tree [1,2,3], return false.

在 RCNN 初步试水取得成功后，研究人员又迅速跟进，针对 RCNN 中的几点不足提出改进，接连推出了 fast-rcnn 和 faster-rcnn。关于这两篇论文，网上相关的文章实在是多如牛毛，因此，本篇博文不打算深入讲解，只是不落俗套地介绍一下它们改进的痛点，基本流程，以及我自己对一些小问题的理解。

在上一篇文章中，我们推导出了 SVM 的目标函数： \[ \underset{(\mathbf{w},b)}{\operatorname{min}} ||\mathbf{w}|| \\ \operatorname{s.t.} \ y_i(\mathbf{w}^T\mathbf{x_i}+b) \ge \delta, \ \ i=1,...,m \] 由于求解过程中，限制条件中的 \(\delta\) 对结果不产生影响，所以简单起见我们把 \(\delta\) 替换成 1。另外，为了之后求解的方便，我们会把原函数中的 \(||\mathbf{w}||\) 换成 \(\frac{1}{2}||\mathbf{w}||^2\)，优化前者跟优化后者，最终的结果是一致的。这样，我们就得到 SVM 最常见的目标函数： \[ \begin{align} &\underset{(\mathbf{w},b)}{\operatorname{min}} \frac{1}{2}\mathbf{w}^2 \tag{1} \\ \operatorname{s.t.} \ y_i (\mathbf{w}^T & \mathbf{x_i}+b) \ge 1, \ i=1,...,m \notag \end{align} \] 现在，我们要开始着手来解这个函数。