在一般的全联接神经网络中,我们通过反向传播算法计算参数的导数。BP 算法本质上可以认为是链式法则在矩阵求导上的运用。但 CNN 中的卷积操作则不再是全联接的形式,因此 CNN 的 BP 算法需要在原始的算法上稍作修改。这篇文章主要讲一下 BP 算法在卷积层和 pooling 层上的应用。
原始的 BP 算法
首先,用两个例子回顾一下原始的 BP 算法。(不熟悉 BP 可以参考How the backpropagation algorithm works,不介意的话可以看我的读书笔记)
最简单的例子
先看一个最简单的例子(偷个懒,搬个手绘图~囧~):
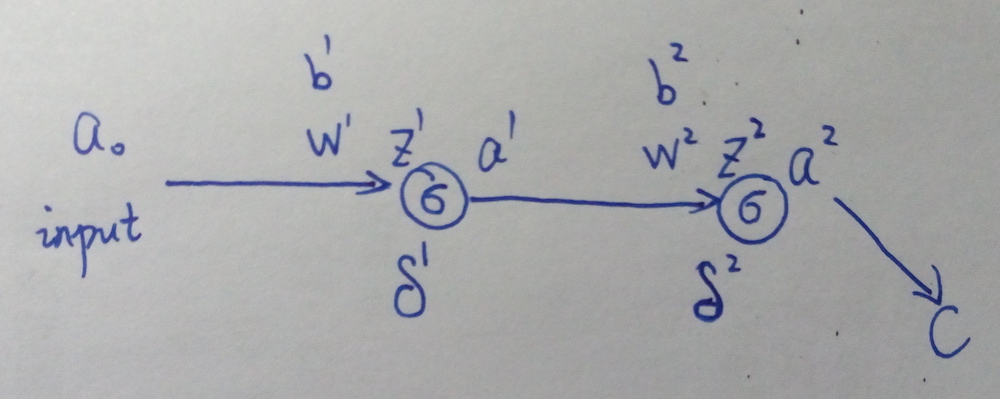
上图中,\(a^l\) 表示第 \(l\) 层的输出(\(a^0\) 就是网络最开始的输入),网络的激活函数假设都是 \(\sigma()\),\(w^l\) 和 \(b^l\) 表示第 \(l\) 层的参数,\(C\) 表示 \(loss\ function\),\(\delta^l\) 表示第 \(l\) 层的误差,\(z^l\) 是第 \(l\) 层神经元的输入,即 \(z^l=w^l a^{l-1}+b^l\),\(a^l=\sigma(z^l)\)。
接下来要用 BP 算法求参数的导数 \(\frac{\partial C}{\partial w}\) 和 \(\frac{\partial C}{\partial b}\)。 \[ \delta^2=\frac{\partial C}{\partial z^2}=\frac{\partial C}{\partial a^2}\frac{\partial a^2}{\partial z^2}=\frac{\partial C}{\partial a^2}\sigma'(z^2) \]
\[ \delta^1=\frac{\partial C}{\partial z^1}=\delta^2\frac{\partial z^2}{\partial a^1}\frac{\partial a^1}{\partial z^1}=\delta^2 w^2\sigma'(z^1) \]
算出这两个误差项后,就可以直接求出导数了: \[ \frac{\partial C}{\partial b^2}=\frac{\partial C}{\partial a^2}\frac{\partial a^2}{\partial z^2}\frac{\partial z^2}{\partial b^2}=\delta^2 \]
\[ \frac{\partial C}{\partial w^2}=\frac{\partial C}{\partial a^2}\frac{\partial a^2}{\partial z^2}\frac{\partial z^2}{\partial w^2}=\delta^2 a^1 \]
\(\frac{\partial C}{\partial b^1}\) 和 \(\frac{\partial C}{\partial w^1}\) 的求法是一样的,这里不在赘述。
次简单的例子
接下来稍微把网络变复杂一点:
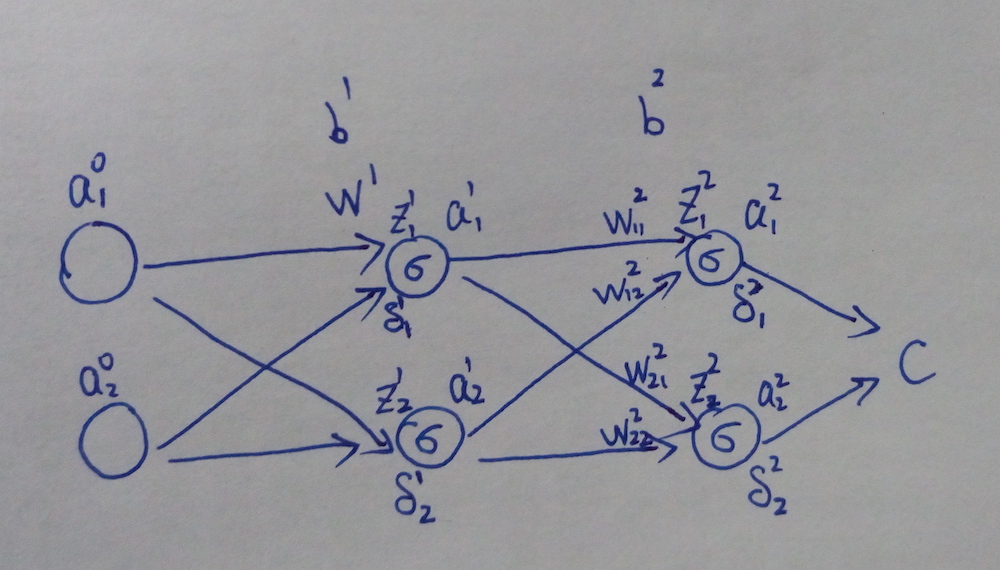
符号的标记和上一个例子是一样的。要注意的是,这里的 \(W^l\) 不再是一个数,而变成一个权重矩阵,\(W_{kj}^l\) 表示第 \(l-1\) 层的第 \(j\) 个神经元到第 \(l\) 层的第 \(k\) 个神经元的权值,如下图所示:
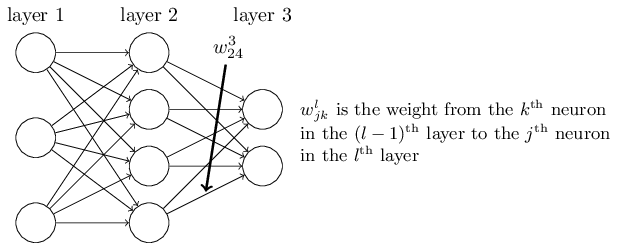
首先,还是要先求出网络的误差 \(\mathbf{\delta}\)。 \[ \delta_1^2=\frac{\partial C}{\partial z_1^2}=\frac{\partial C}{\partial a_1^2}\sigma'(z_1^2) \]
\[ \delta_2^2=\frac{\partial C}{\partial z_2^2}=\frac{\partial C}{\partial a_2^2}\sigma'(z_2^2) \]
由此得到: \[ \delta^2=\begin{bmatrix} \delta_1^2 \\ \delta_2^2 \end{bmatrix}=\begin{bmatrix} \frac{\partial C}{\partial a_1^2} \\ \frac{\partial C}{\partial a_2^2} \end{bmatrix} \odot \begin{bmatrix} \sigma'(z_1^2) \\ \sigma'(z_2^2) \end{bmatrix} \] \(\odot\) 表示 elementwise 运算。
接着要根据 \(\delta^2\) 计算前一层的误差 \(\delta^1\)。 \[ \begin{align} \delta_1^1=\frac{\partial C}{\partial z_1^1}=&\frac{\partial C}{\partial a_1^2}\sigma'(z_1^2)\frac{\partial z_1^2}{\partial a_1^1}\frac{\partial a_1^1}{\partial z_1^1}+ \notag \\ &\frac{\partial C}{\partial a_2^2}\sigma'(z_2^2)\frac{\partial z_2^2}{\partial a_1^1}\frac{\partial a_1^1}{\partial z_1^1} \notag \\ =&\frac{\partial C}{\partial a_1^2}\sigma'(z_1^2)W_{11}^2\sigma'(z_1^1)+\tag{1} \\ &\frac{\partial C}{\partial a_2^2}\sigma'(z_2^2)W_{21}^2\sigma'(z_1^1) \notag \\ =&\begin{bmatrix}\frac{\partial C}{\partial a_1^2}\sigma'(z_1^2) & \frac{\partial C}{\partial a_2^2}\sigma'(z_2^2) \end{bmatrix} \begin{bmatrix} W_{11}^2 \\ W_{21}^2 \end{bmatrix} \odot \begin{bmatrix} \sigma'(z_1^1) \end{bmatrix} \notag \end{align} \] 同理,\(\delta_2^1=\begin{bmatrix}\frac{\partial C}{\partial a_1^2}\sigma'(z_1^2) & \frac{\partial C}{\partial a_2^2}\sigma'(z_2^2) \end{bmatrix} \begin{bmatrix} W_{12}^2 \\ W_{22}^2 \end{bmatrix} \odot \begin{bmatrix} \sigma'(z_2^1) \end{bmatrix}\)。
这样,我们就得到第 1 层的误差项: \[ \delta^1=\begin{bmatrix} W_{11}^2 & W_{21}^2 \\ W_{12}^2 & W_{22}^2 \end{bmatrix} \begin{bmatrix} \frac{\partial C}{\partial z_1^2} \\ \frac{\partial C}{\partial z_2^2} \end{bmatrix} \odot \begin{bmatrix} \sigma'(z_1^1) \\ \sigma'(z_2^1) \end{bmatrix}={W^{2}}^T\delta^2 \odot \sigma'(z^1) \tag{2} \] 然后,根据误差项计算导数: \[ \frac{\partial C}{\partial b_j^2}=\frac{\partial C}{\partial z_j^2}\frac{\partial z_j^2}{\partial b_j^2}=\delta_j^2 \\ \frac{\partial C}{\partial w_{jk}^2}=\frac{\partial C}{\partial z_j^2}\frac{\partial z_j^2}{\partial w_{jk}^2}=a_k^{1}\delta_j^2 \\ \frac{\partial C}{\partial b_j^1}=\frac{\partial C}{\partial z_j^1}\frac{\partial z_j^1}{\partial b_j^1}=\delta_j^1 \\ \frac{\partial C}{\partial w_{jk}^1}=\frac{\partial C}{\partial z_j^1}\frac{\partial z_j^1}{\partial w_{jk}^1}=a_k^{0}\delta_j^1 \]
BP 算法的套路
在 BP 算法中,我们计算的误差项 \(\delta^l\) 其实就是 \(loss\ function\) 对 \(z^l\) 的导数 \(\frac{\partial C}{\partial z^l}\),有了该导数后,根据链式法则就可以比较容易地求出 \(\frac{\partial C}{\partial W^l}\) 和 \(\frac{\partial C}{\partial b^l}\)。
CNN 中的 BP 算法
之所以要「啰嗦」地回顾普通的 BP 算法,主要是为了熟悉一下链式法则,因为这一点在理解 CNN 的 BP 算法时尤为重要。
下面就来考虑如何把之前的算法套路用在 CNN 网络中。
CNN 的难点在于卷积层和 pooling 层这两种很特殊的结构,因此下面重点分析这两种结构的 BP 算法如何执行。
卷积层
假设我们要处理如下卷积操作: \[ \left( \begin{array}{ccc} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{array} \right) * \left( \begin{array}{ccc} w_{11}&w_{12}\\ w_{21}&w_{22} \end{array} \right) = \left( \begin{array}{ccc} z_{11}&z_{12}\\ z_{21}&z_{22} \end{array} \right) \] 这个操作咋一看完全不同于全联接层的操作,这样,想套一下 BP 算法都不知从哪里入手。但是,如果把卷积操作表示成下面的等式,问题就清晰多了(卷积操作一般是要把卷积核旋转 180 度再相乘的,不过,由于 CNN 中的卷积参数本来就是学出来的,所以旋不旋转,关系其实不大,这里默认不旋转): \[ z_{11} = a_{11}w_{11} + a_{12}w_{12} + a_{21}w_{21} + a_{22}w_{22} \\ z_{12} = a_{12}w_{11} + a_{13}w_{12} + a_{22}w_{21} + a_{23}w_{22} \\ z_{21} = a_{21}w_{11} + a_{22}w_{12} + a_{31}w_{21} + a_{32}w_{22} \\ z_{22} = a_{22}w_{11} + a_{23}w_{12} + a_{32}w_{21} + a_{33}w_{22} \] 更进一步,我们还可以把上面的等式表示成下图:
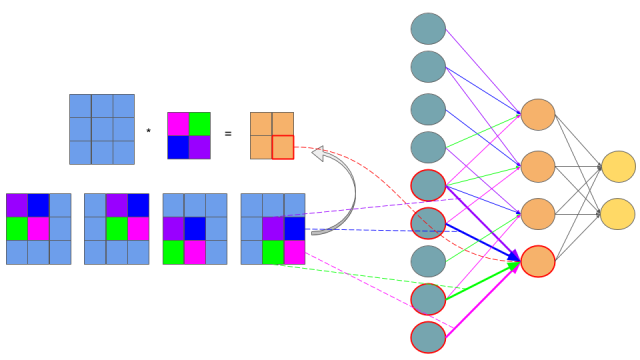
上图的网络结构中,左边青色的神经元表示 \(a_{11}\) 到 \(a_{33}\),中间橙色的表示 \(z_{11}\) 到 \(z_{22}\)。需要注意的是,青色和橙色神经元之间的权值连接用了不同的颜色标出,紫色线表示 \(w_{11}\),蓝色线表示 \(w_{12}\),依此类推。这样一来,如果你熟悉 BP 链式法则的套路的话,你可能已经懂了卷积层的 BP 是怎么操作的了。因为卷积层其实就是一种特殊的连接层,它是部分连接的,而且参数也是共享的。
假设上图中,\(z\) 这一层神经元是第 \(l\) 层,即 \(z=z^{l}\),\(a=a^{l-1}\)。同时假设其对应的误差项 \(\delta^{l}=\frac{\partial C}{\partial z^{l}}\) 我们已经算出来了。下面,按照 BP 的套路,我们要根据 \(\delta^{l}\) 计算 \(\delta^{l-1}\)、\(\frac{\partial C}{\partial w^l}\) 和 \(\frac{\partial C}{\partial b^l}\) 。
卷积层的误差项 \(\delta^{l-1}\)
首先计算 \(\delta^{l-1}\)。假设上图中的 \(a^{l-1}\) 是前一层经过某些操作(可能是激活函数,也可能是 pooling 层等,但不管是哪种操作,我们都可以用 \(\sigma()\) 来表示)后得到的响应,即 \(a^{l-1}=\sigma(z^{l-1})\)。那么,根据链式法则: \[ \delta^{l-1}=\frac{\partial C}{\partial z^{l-1}}=\frac{\partial C}{\partial z^{l}}\frac{\partial z^l}{\partial a^{l-1}}\frac{\partial a^{l-1}}{\partial z^{l-1}}=\delta^l \frac{\partial z^l}{\partial a^{l-1}} \odot \sigma'(z^{l-1}) \tag{3} \] 对照上面的例子,\(z^{l-1}\) 应该是一个 9 维的向量,所以 \(\sigma'(z^{l-1})\) 也是一个向量,根据之前 BP 的套路,这里需要 \(\odot\) 操作。
这里的重点是要计算 \(\frac{\partial z^l}{\partial a^{l-1}}\),这也是卷积层区别于全联接层的地方。根据前面展开的卷积操作的等式,这个导数其实比全联接层更容易求。以 \(a_{11}^{l-1}\) 和 \(a_{12}^{l-1}\) 为例(简洁起见,下面去掉右上角的层数符号 \(l\)): \[ \begin{align} \nabla a_{11} = & \frac{\partial C}{\partial z_{11}} \frac{\partial z_{11}}{\partial a_{11}}+ \frac{\partial C}{\partial z_{12}}\frac{\partial z_{12}}{\partial a_{11}}+ \frac{\partial C}{\partial z_{21}}\frac{\partial z_{21}}{\partial a_{11}} + \frac{\partial C}{\partial z_{22}}\frac{\partial z_{22}}{\partial a_{11}} \notag \\ =& \delta_{11}w_{11} \notag \end{align} \] \[ \begin{align} \nabla a_{12} =& \frac{\partial C}{\partial z_{11}}\frac{\partial z_{11}}{\partial a_{12}} + \frac{\partial C}{\partial z_{12}}\frac{\partial z_{12}}{\partial a_{12}} + \frac{\partial C}{\partial z_{21}}\frac{\partial z_{21}}{\partial a_{12}} + \frac{\partial C}{\partial z_{22}}\frac{\partial z_{22}}{\partial a_{12}} \notag \\ =&\delta_{11}w_{12} + \delta_{12}w_{11} \notag \end{align} \]
(\(\nabla a_{ij}\) 表示 \(\frac{\partial C}{\partial a_{ij}}\)。如果这两个例子看不懂,证明对之前 BP 例子中的(1)式理解不够,请先复习普通的 BP 算法。)
其他 \(\nabla a_{ij}\) 的计算,道理相同。
之后,如果你把所有式子都写出来,就会发现,我们可以用一个卷积运算来计算所有 \(\nabla a_{ij}^{l-1}\): \[ \left( \begin{array}{ccc} 0&0&0&0 \\ 0&\delta_{11}& \delta_{12}&0 \\ 0&\delta_{21}&\delta_{22}&0 \\ 0&0&0&0 \end{array} \right) * \left( \begin{array}{ccc} w_{22}&w_{21}\\ w_{12}&w_{11} \end{array} \right) = \left( \begin{array}{ccc} \nabla a_{11}&\nabla a_{12}&\nabla a_{13} \\ \nabla a_{21}&\nabla a_{22}&\nabla a_{23}\\ \nabla a_{31}&\nabla a_{32}&\nabla a_{33} \end{array} \right) \] 这样一来,(3)式可以改写为: \[ \delta^{l-1}=\frac{\partial C}{\partial z^{l-1}}=\delta^l * rot180(W^l) \odot \sigma'(z^{l-1}) \tag{4} \] (4)式就是 CNN 中误差项的计算方法。注意,跟原始的 BP 不同的是,这里需要将后一层的误差 \(\delta^l\) 写成矩阵的形式,并用 0 填充到合适的维度。而且这里不再是跟矩阵 \({W^l}^T\) 相乘,而是先将 \(W^l\) 旋转 180 度后,再跟其做卷积运算。
卷积层的导数 \(\frac{\partial C}{\partial w^l}\) 和 \(\frac{\partial C}{\partial b^l}\)
这两项的计算也是类似的。假设已经知道当前层的误差项 \(\delta^l\),参考之前 \(\nabla a_{ij}\) 的计算,可以得到: \[ \begin{align} \nabla w_{11}=&\frac{\partial C}{\partial z_{11}} \frac{\partial z_{11}}{\partial w_{11}}+ \frac{\partial C}{\partial z_{12}}\frac{\partial z_{12}}{\partial w_{11}}+ \frac{\partial C}{\partial z_{21}}\frac{\partial z_{21}}{\partial w_{11}} + \frac{\partial C}{\partial z_{22}}\frac{\partial z_{22}}{\partial w_{11}} \notag \\ =&\delta_{11}a_{11}+\delta_{12}a_{12}+\delta_{21}a_{21}+\delta_{22}a_{22} \notag \end{align} \]
\[ \begin{align} \nabla w_{12}=&\frac{\partial C}{\partial z_{11}} \frac{\partial z_{11}}{\partial w_{12}}+ \frac{\partial C}{\partial z_{12}}\frac{\partial z_{12}}{\partial w_{12}}+ \frac{\partial C}{\partial z_{21}}\frac{\partial z_{21}}{\partial w_{12}} + \frac{\partial C}{\partial z_{22}}\frac{\partial z_{22}}{\partial w_{12}} \notag \\ =&\delta_{11}a_{12}+\delta_{12}a_{13}+\delta_{21}a_{22}+\delta_{22}a_{23} \notag \end{align} \]
其他 \(\nabla w_{ij}\) 的计算同理。
跟 \(\nabla a_{ij}\) 一样,我们可以用矩阵卷积的形式表示: \[ \left( \begin{array}{ccc} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{array} \right) * \left( \begin{array}{ccc} \delta_{11}& \delta_{12}\\ \delta_{21}&\delta_{22}\end{array} \right) = \left( \begin{array}{ccc} \nabla w_{11}&\nabla w_{12}\\ \nabla w_{21}&\nabla w_{22} \end{array} \right) \] 这样就得到了 \(\frac{\partial C}{\partial w^l}\) 的公式: \[ \frac{\partial C}{\partial w^l}=a^{l-1}*\delta^l \tag{5} \] 对于 \(\frac{\partial C}{\partial b^l}\),我参考了文末的链接,但对其做法仍然不太理解,我觉得在卷积层中,\(\frac{\partial C}{\partial b^l}\) 和一般的全联接层是一样的,仍然可以用下面的式子得到: \[ \frac{\partial C}{\partial b^l}=\delta^l \tag{6} \] 理解不一定对,所以这一点上大家还是参考一下其他资料。
pooling 层
跟卷积层一样,我们先把 pooling 层也放回网络连接的形式中:
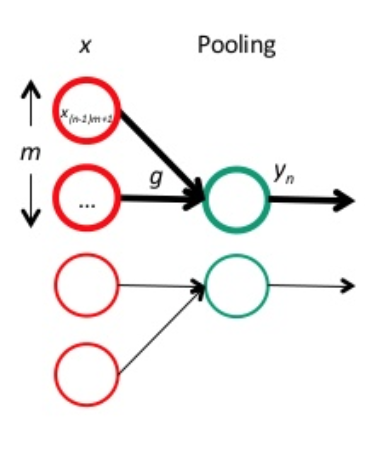
红色神经元是前一层的响应结果,一般是卷积后再用激活函数处理。绿色的神经元表示 pooling 层。很明显,pooling 主要是起到降维的作用,而且,由于 pooling 时没有参数需要学习,因此,当得到 pooling 层的误差项 \(\delta^l\) 后,我们只需要计算上一层的误差项 \(\delta^{l-1}\) 即可。要注意的一点是,由于 pooling 一般会降维,因此传回去的误差矩阵要调整维度,即 \(upsample\)。这样,误差传播的公式原型大概是:
\(\delta^{l-1}=upsample(\delta^l) \odot \sigma'(z^{l-1})\)。
下面以最常用的 average pooling 和 max pooling 为例,讲讲 \(upsample(\delta^l)\) 具体要怎么处理。
假设 pooling 层的区域大小为 \(2 \times 2\),pooling 这一层的误差项为: \[ \delta^l= \left( \begin{array}{ccc} 2 & 8 \\ 4 & 6 \end{array} \right) \] 首先,我们先把维度还原到上一层的维度: \[ \left( \begin{array}{ccc} 0 & 0 & 0 & 0 \\ 0 & 2 & 8 & 0 \\ 0 & 4 & 6 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right) \] 在 average pooling 中,我们是把一个范围内的响应值取平均后,作为一个 pooling unit 的结果。可以认为是经过一个 average() 函数,即 \(average(x)=\frac{1}{m}\sum_{k=1}^m x_k\)。在本例中,\(m=4\)。则对每个 \(x_k\) 的导数均为:
\[\frac{\partial average(x)}{\partial x_k}=\frac{1}{m}\]
因此,对 average pooling 来说,其误差项为: \[ \begin{align} \delta^{l-1}=&\delta^l \frac{\partial average}{\partial x} \odot \sigma'(z^{l-1}) \notag \\ =&upsample(\delta^l) \odot \sigma'(z^{l-1}) \tag{7} \\ =&\left( \begin{array}{ccc} 0.5&0.5&2&2 \\ 0.5&0.5&2&2 \\ 1&1&1.5&1.5 \\ 1&1&1.5&1.5 \end{array} \right)\odot \sigma'(z^{l-1}) \notag \end{align} \] 在 max pooling 中,则是经过一个 max() 函数,对应的导数为: \[ \frac{\partial \max(x)}{\partial x_k}=\begin{cases} 1 & if\ x_k=max(x) \\ 0 & otherwise \end{cases} \] 假设前向传播时记录的最大值位置分别是左上、右下、右上、左下,则误差项为: \[ \delta^{l-1}=\left( \begin{array}{ccc} 2&0&0&0 \\ 0&0& 0&8 \\ 0&4&0&0 \\ 0&0&6&0 \end{array} \right) \odot \sigma'(z^{l-1}) \tag{8} \]