这篇论文是要解决 person re-identification 的问题。所谓 person re-identification,指的是在不同的场景下识别同一个人(如下图所示)。这里的难点是,由于不同场景下的角度、背景亮度等等因素的差异,同一个人的图像变化非常大,因而不能使用一般的图像分类的方法。论文采用了一种相似性度量的方法来促使神经网络学习出图像的特征,并根据特征向量的欧式距离来确定相似性。除此之外,论文通过对网络的训练过程进行分析,提出了一种计算效率更高的模型训练方法。

论文方法
相似性模型
论文采用的度量相似性的方法基于一个简单的想法:相同类型图片(同一个人)的特征之间的距离要小于不同类型的特征。假设我们有一些训练样本,现在把它们组织成三元组的形式 \({O_i}=<O_i^1,O_i^2,O_i^3>\),其中 \(O_i^1\) 和 \(O_i^2\) 表示属于同一类(匹配)的样本,\(O_i^1\) 和 \(O_i^3\) 表示不匹配的样本。设网络的参数为 \(W=\{W_j\}\),\(F_W(I)\) 表示图像 \(I\) 的特征向量,则我们的目标是使下面的不等式成立: \[ \begin{align} ||F_W(O_i^1)-F_W(O_i^2)||^2<||F_W(O_i^1)-F_W(O_i^3)||^2 \tag{2} \end{align} \] 基于此,论文给出如下目标函数: \[ \begin{align} f(W,O)=\sum_{i=1}^n{\max{\{||F_W(O_i^1)-F_W(O_i^2)||^2-||F_W(O_i^1)-F_W(O_i^3)||^2, C \}}} \tag{3} \end{align} \] 其中,\(C\) 被设为 -1。
网络结构
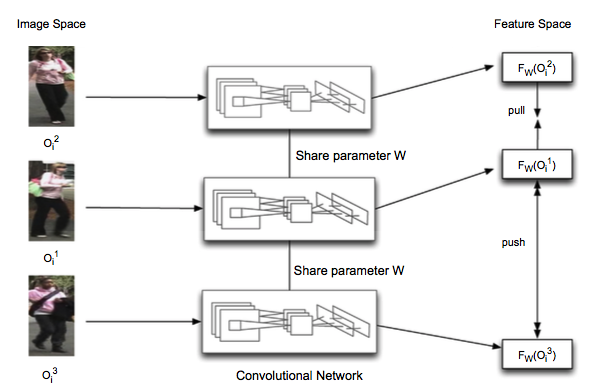
这三个子网络是共享参数的,目标函数是要让 \(F_W(O_i^2)\) 和 \(F_W(O_i^1)\) 靠近,而 \(F_W(O_i^3)\) 远离前两个特征向量。
训练算法
设 \(d(W,O_i)=||F_W(O_i^1)-F_W(O_i^2)||^2-||F_W(O_i^1)-F_W(O_i^3)||^2\),基于 (3) 式,我们可以得到梯度下降的导数公式: \[ \begin{align} & \frac{\partial f}{\partial W_j}=\sum_{O_i}{h(O_i)} \tag{7} \\ & h(O_i)=\begin{cases} \frac{\partial d(W,O_i)}{\partial W_j} & if\ d(W,O_i)>C \\ 0 & otherwise \end{cases} \tag{8} \end{align} \]
\[ \begin{align} \frac{\partial d(W,O_i)}{\partial W_j}=&2(F_W(O_i^1)-F_W(O_i^2))\frac{\partial F_W(O_i^1)- \partial F_W(O_i^2)}{\partial W_j} \notag \\ &-2(F_W(O_i^1)-F_W(O_i^3))\frac{\partial F_W(O_i^1)- \partial F_W(O_i^3)}{\partial W_j} \tag{9} \end{align} \]
由此可知,每次梯度下降时,我们只需要计算出每个 triplet 的 \(F_W(O_i^1)\)、\(F_W(O_i^2)\)、\(F_W(O_i^3)\) 和 \(\frac{\partial F_W(O_i^1)}{\partial W_j}\)、\(\frac{\partial F_W(O_i^2)}{\partial W_j}\)、\(\frac{\partial F_W(O_i^3)}{\partial W_j}\),就可以得到 \(W_j\) 的导数。这种导数计算方式是基于 triplet 的,每对样本需要计算三次前向和三次后向。由此可以得到论文中的算法 1:

然而,在实际训练时,一张图片可能在一个 batch 的多个 triplet 中出现,因此可以用一些技巧来减少一些重复计算的工作。重新审视导数的计算流程: \[ \begin{align} \frac{\partial f}{\partial W}=\sum_{O_i}(\frac{\partial f}{\partial F_W(O_i^1)}\frac{\partial F_W(O_i^1)}{\partial W_j} + \frac{\partial f}{\partial F_W(O_i^2)}\frac{\partial F_W(O_i^2)}{\partial W_j} + \frac{\partial f}{\partial F_W(O_i^3)}\frac{\partial F_W(O_i^3)}{\partial W_j}) \notag \end{align} \] 可以发现,重复计算的地方在于 \(\frac{\partial F_W(O_i^1)}{\partial W_j}\)、\(\frac{\partial F_W(O_i^2)}{\partial W_j}\)、\(\frac{\partial F_W(O_i^3)}{\partial W_j}\) 这些项,而且这些项也只跟对应的输入图像有关,所以,我们的想法是把这些可以重复使用的项提取出来。 假设一个训练 batch 中的图片集合为 \(\{I_k^{'}\}=\{O_i^1\} \cup \{O_i^2\} \cup \{O_i^3\}\),\(m\) 为图片数量,则针对一张图片的导数计算公式为: \[ \begin{align} \sum_{O_i}\frac{\partial f}{\partial F_W(I_i)}\frac{\partial F_W(I_i)}{W_j}=\frac{\partial F_W(I_i)}{W_j}\sum_{O_i}\frac{\partial f}{\partial F_W(I_i)}\notag \end{align} \] 因此整个 batch 上的导数如下: \[ \begin{align} \frac{\partial f}{\partial W}=\sum_{i=1}^m\{\frac{\partial F_W(I_i)}{W_j}\sum_{O_i}\frac{\partial f}{\partial F_W(I_i)}\} \tag{18} \end{align} \] \(\frac{\partial F_W(I_i)}{W_j}\) 只跟输入 \(I_i\) 有关,因此接下来要解决 \(\sum_{O_i}\frac{\partial f}{\partial F_W(I_i)}\) 的计算问题。后者的计算是跟 triplet 相关的: \[ \begin{align} \frac{\partial f}{\partial F_W(I_K^{'})}=\sum_{i=1}^{n}\frac{\partial \max\{||F_W(O_i^1)-F_W(O_i^2)||^2-||F_W(O_i^1)-F_W(O_i^3)||^2,C\}}{\partial F_W(I_K^{'})} \tag{19} \end{align} \] 由此我们可以得出论文中的算法 3:

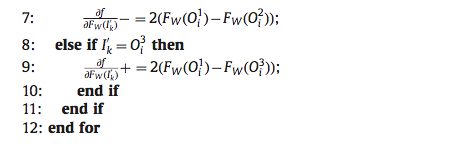
在此基础上,将 \(\frac{\partial f}{\partial F_W(I_K^{'})}\) 代入到 (18) 式,就得到了一个 batch 上的导数计算公式,即论文中的算法 2:

注意到,我们已经把原来基于 triplet 的计算方式转变为基于 image 的方式。后者可以大大减少计算量,我们只需要先计算出每张图片对应的 \(F_W(I_K^{'})\) 和 \(\frac{\partial F_W{I_K^{'}}}{\partial W_j}\),剩下的工作就是根据算法 2 计算出最终的导数。因此,这种计算方式使得整体的运算量只跟图片的数量有关。
最后要考虑的是样本生成的问题。最简单的想法是从所有可能的 triplet 组合中,随机挑选出若干的 triplet用于训练,但这种做法存在一个问题,考虑到数据集中的类别可能很大,因此所有 triplet 中包含的图片类别可能都是不同的,换句话说,网络在每次迭代时,处理的图片可能都是完全不同的,论文认为这种方式不利于参数的收敛。因此论文采用如下的 triplet 生成策略:在每轮迭代中,首先挑选出若干的类别(每个类别代表一个人),然后,对每个类别中的图片,从同类别的其他图片中随机选一张组成正样本对,从不同类别的图片中随机选一张组成负样本对。这种做法的优点在于,它的训练样本是梯度下降的时候动态生成的,假设显存中可以存放 300 张图片,那么对于最简单的 triplet 生成方法,可能只能放 100 对训练样本,但论文采用的生成策略,可以先从选定的几个类别中选出 300 张图片,然后进行 triplet 组合,等一次迭代训练完成后,再根据这 300 张图片随机生成另一种 triplet 组合。所以,这种方法不仅可以让网络更好地学习出样本对之间的距离约束关系,而且减少了频繁的 IO 操作。
下面给出完整的算法:
