高中的时候我们便学过一维正态(高斯)分布的公式: \[ N(x|u,\sigma^2)=\frac{1}{\sqrt{2\pi \sigma^2}}exp[-\frac{1}{2\sigma^2}(x-u)^2] \] 拓展到高维时,就变成: \[ N(\overline x | \overline u, \Sigma)=\frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma|^{1/2}}exp[-\frac{1}{2}(\overline x-\overline u)^T\Sigma^{-1}(\overline x-\overline u)] \] 其中,\(\overline x\) 表示维度为 D 的向量,\(\overline u\) 则是这些向量的平均值,\(\Sigma\) 表示所有向量 \(\overline x\) 的协方差矩阵。
本文只是想简单探讨一下,上面这个高维的公式是怎么来的。
二维的情况
为了简单起见,本文假设所有变量都是相互独立的。即对于概率分布函数 \(f(x_0,x_1,…,x_n)\) 而言,有 \(f(x_0,x_1,…,x_n)=f(x_0)f(x_1)f(x_n)\) 成立。
现在,我们用一个二维的例子推出上面的公式。
假设有很多变量 \(\overline x=\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\),它们的均值为 \(\overline u=\begin{bmatrix} u_1 \\ u_2 \end{bmatrix}\),方差为 \(\overline \sigma=\begin{bmatrix} \sigma_1 \\ \sigma_2 \end{bmatrix}\)。
由于 \(x_1\),\(x_2\) 是相互独立的,所以,\(\overline x\) 的高斯分布函数可以表示为: \[ \begin{eqnarray} f(\overline x) &=& f(x_1,x_2) \\ &=& f(x_1)f(x_2) \\ &=& \frac{1}{\sqrt{2\pi \sigma_1^2}}exp(-\frac{1}{2}(\frac{x_1-u_1}{\sigma_1})^2) \times \frac{1}{\sqrt{2\pi \sigma_2^2}}exp(-\frac{1}{2}(\frac{x_2-u_2}{\sigma_2})^2) \\ &=&\frac{1}{(2\pi)^{2/2}(\sigma_1^2 \sigma_2^2)^{1/2}}exp(-\frac{1}{2}[(\frac{x_1-u_1}{\sigma_1})^2+(\frac{x_2-u_2}{\sigma_2})^2]) \end{eqnarray} \] 接下来,为了推出文章开篇的高维公式,我们要想办法得到协方差矩阵 \(\Sigma\)。
对于二维的向量 \(\overline x\) 而言,其协方差矩阵为: \[ \begin{eqnarray} \Sigma&=&\begin{bmatrix} \sigma_{11} & \sigma_{12} \\ \sigma_{12} & \sigma_{22} \end{bmatrix} \\ &=&\begin{bmatrix} \sigma_1^2 & \sigma_{12} \\ \sigma_{21} & \sigma_{2}^2 \end{bmatrix} \\ \end{eqnarray} \] (不熟悉协方差矩阵的请查找其他资料或翻看我之前的文章)
由于 \(x_1\),\(x_2\) 是相互独立的,所以 \(\sigma_{12}=\sigma_{21}=0\)。这样,\(\Sigma\) 退化成 \(\begin{bmatrix} \sigma_1^2 & 0 \\ 0 & \sigma_{2}^2 \end{bmatrix}\)。
则 \(\Sigma\) 的行列式 \(|\Sigma|=\sigma_1^2 \sigma_2^2\),代入公式 (4) 就可以得到: \[ f(\overline x)=\frac{1}{(2\pi)^{2/2}|\Sigma|^{1/2}}exp(-\frac{1}{2}[(\frac{x_1-u_1}{\sigma_1})^2+(\frac{x_2-u_2}{\sigma_2})^2]) \] 这样一来,我们已经推出了公式的左半部分,下面,开始处理右面的 \(exp\) 函数。
原始的高维高斯函数的 \(exp\) 函数为:\(exp[-\frac{1}{2}(\overline x-\overline u)^T\Sigma^{-1}(\overline x-\overline u)]\),根据前面算出来的 \(\Sigma\),我们可以求出它的逆:\(\Sigma^{-1}=\frac{1}{\sigma_1^2 \sigma_2^2} \begin{bmatrix} \sigma_2^2 & 0 \\ 0 & \sigma_1^2 \end{bmatrix}\)。
接下来根据这个二维的例子,将原始的 \(exp()\) 展开: \[ \begin{eqnarray} exp[-\frac{1}{2}(\overline x-\overline u)^T\Sigma^{-1}(\overline x-\overline u)] &=& exp[-\frac{1}{2} \begin{bmatrix} x_1-u_1 \ \ \ x_2-u_2 \end{bmatrix} \frac{1}{\sigma_1^2 \sigma_2^2} \begin{bmatrix} \sigma_2^2 & 0 \\ 0 & \sigma_1^2 \end{bmatrix} \begin{bmatrix} x_1-u_1 \\ x_2-u_2 \end{bmatrix}] \\ &=&exp[-\frac{1}{2} \begin{bmatrix} x_1-u_1 \ \ \ x_2-u_2 \end{bmatrix} \frac{1}{\sigma_1^2 \sigma_2^2} \begin{bmatrix} \sigma_2^2(x_1-u_1) \\ \sigma_1^2(x_2-u_2) \end{bmatrix}] \\ &=&exp[-\frac{1}{2\sigma_1^2 \sigma_2^2}[\sigma_2^2(x_1-u_1)^2+\sigma_1^2(x_2-u_2)^2]] \\ &=&exp[-\frac{1}{2}[\frac{(x_1-u_1)^2}{\sigma_1^2}+\frac{(x_2-u_2)^2}{\sigma_2^2}]] \end{eqnarray} \] 展开到最后,发现推出了公式 (4)。说明原公式 \(N(\overline x | \overline u, \Sigma)=\frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma|^{1/2}}exp[-\frac{1}{2}(\overline x-\overline u)^T\Sigma^{-1}(\overline x-\overline u)]\) 是成立的。你也可以将上面展开的过程逆着推回去,一样可以从例子中的公式 (4) 推出多维高斯公式。
函数图像
知道多维的公式后,下面再简单比较一下一维和二维的图像区别。
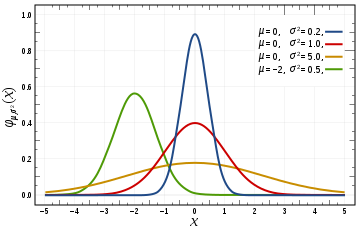
上图展示的是 4 个一维高斯函数的图像。高斯函数是一个对称的山峰状,山峰的中心是均值 \(u\),山峰的「胖瘦」由标准差 \(\sigma\) 决定,如果 \(\sigma\) 越大,证明数据分布越广,那么山峰越「矮胖」,反之,则数据分布比较集中,因此很大比例的数据集中在均值附近,山峰越「瘦高」。在偏离均值 \(u\) 三个 \(\sigma\) 的范围外,数据出现的概率几乎接近 0,因此这一部分的函数图像几乎与 x 轴重合。
下面看二维的例子:
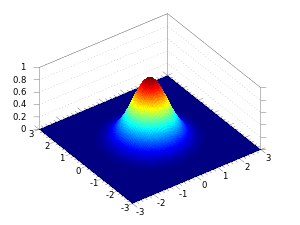
有了一维图像的例子,二维图像就可以类比出来了。如果说,一维只是山峰的一个横截面,那么二维则是一个完整的有立体感的山峰。山峰的「中心」和「胖瘦」和一维的情况是一致的,而且,对于偏离中心较远的位置,数据出现的概率几乎为 0,因此,函数图像在这些地方就逐渐退化成「平原」了。
参数估计
另外,如果给定了很多数据点,并且知道它们服从某个高斯分布,我们要如何求出高斯分布的参数(\(\mu\) 和 \(\Sigma\))呢?
当然,估计模型参数的方法有很多,最常用的就是极大似然估计。
简单起见,拿一维的高斯模型举例。假设我们有很多数据点:\((x_1, x_2, x_3, \dots, x_m)\),它们的均值是\(\tilde u\)。一维高斯函数是:\(p(x|\mu, \sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(x-\mu)^2}{2\sigma^2})\)
首先,我们先写出似然函数: \[ \begin{eqnarray} f(x_1, x_2, \dots, x_m)&=&\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(x_i-\tilde \mu)^2}{2\sigma^2}) \\ &=&(2\pi \sigma^2)^{-\frac{m}{2}}exp(-\frac{\sum_{i=1}^n{(x_i-\tilde \mu)^2}}{2\sigma^2}) \end{eqnarray} \] 然后取对数: \[ \ln{f(x_1, x_2, \dots, x_m)}=-\frac{m}{2}\ln{(2\pi \sigma^2)}-\frac{1}{2\sigma^2}\sum_{i=1}^n{(x_i-\tilde \mu)^2} \] 求出导数,令导数为 0 得到似然方程: \[ \frac{\partial \ln f}{\partial \overline \mu}=\frac{1}{\sigma^2}\sum_{i=1}^{n}{(x_i-\tilde \mu)}=0 \]
\[ \frac{\partial \ln{f}}{\partial \sigma}=-\frac{m}{\sigma}+\frac{1}{\sigma^3}\sum_{i=1}^n{(x_i-\tilde \mu)}=0 \]
我们可以求出:\(\mu=\frac{1}{m}\sum_{i=1}^m{(x_i-\tilde \mu)}\),\(\sigma=\sqrt{\frac{1}{m}\sum_{i=1}^m{(x_i-\tilde \mu)^2}}\),可以看到,这其实就是高斯函数中平均值和标准差的定义。
对于高维的情况,平均值和协方差矩阵也可以用类似的方法计算出来。
总结
本文只是从一个简单的二维例子出发,来说明多维高斯公式的来源。在 PRML 的书中,推导的过程更加全面,也复杂了许多,想深入学习多维高斯模型的还是参考教材为准。
重新对比一维和多维的公式: \[ N(x|u,\sigma^2)=\frac{1}{\sqrt{2\pi \sigma^2}}exp[-\frac{1}{2\sigma^2}(x-u)^2] \]
\[ N(\overline x | \overline u, \Sigma)=\frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma|^{1/2}}exp[-\frac{1}{2}(\overline x-\overline u)^T\Sigma^{-1}(\overline x-\overline u)] \]
其实二者是等价的。一维中,我们针对的是一个数,多维时,则是针对一个个向量求分布。如果向量退化成一维,则多维公式中的 \(D=1\),\(\Sigma=\sigma^2\),\(\Sigma^{-1}=\frac{1}{\sigma^2}\),这时多维公式就退化成一维的公式。所以,在多维的公式中,我们可以把 \(\Sigma\) 当作是样本向量的标准差。