(本文是根据 neuralnetworksanddeeplearning 这本书的第一章 Using neural nets to recognize handwritten digits 整理而成的读书笔记,根据个人口味做了删减)
对于人类来说,识别下面的数字易如反掌,但对计算机而言,却不是一个简单的任务。
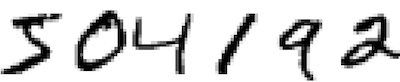
在我们的大脑中,有一块跟视觉相关的皮层 V1,这里面包含着数以百万计的神经元,而这些神经元之间的连接,更是达到了数以亿计。在漫长的进化过程中,大自然将人类的大脑训练成了一个「超级计算机」,使它可以轻易地读懂、看懂、听懂很多目前的计算机仍然难以处理的问题。在本章中,作者介绍了一种可以帮助计算机识别手写体的程序:神经网络「neural network」。
首先,我们从神经网络的几个基本概念讲起。
Perceptrons
Perceptrons,中文译为感知器,最早由科学家Frank Rosenblatt于上个世纪 50 至 60 年代提出。在现代神经网络中,Perceptrons 已经用得很少了(更多地使用 sigmoid neuron 等神经元模型)。但要了解 sigmoid neuron 怎么来的,就有必要先弄清楚 Perceptrons。
举例来说,最简单的 Perceptrons 类似如下结构:
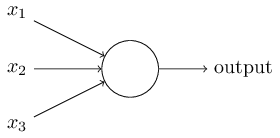
它接受三个输入 \(x_1\)、\(x_2\)、\(x_3\),输出 0 或者 1。为了衡量每个输入的重要程度,Rosenblatt 引入了权重的概念,假设 \(w_1\)、\(w_2\)、\(w_3\) 分别对应 \(x_1\)、\(x_2\)、\(x_3\),那么,我们可以得到 Perceptrons 的输出为: \[ output=\begin{cases} 0 &if \ \ \sum_{j}{w_j x_j} <= threshold \\\\ 1 &if \ \ \sum_{j}{w_j x_j} > threshold \end{cases} \] 当然,Perceptrons 在处理较复杂的任务的时候,其结构也会更加复杂,比如:
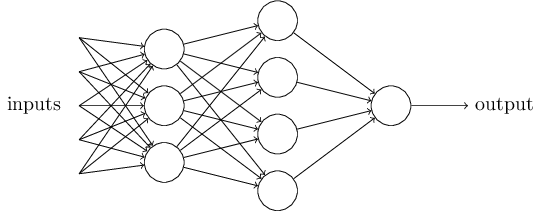
在这个网络中,Perceptrons 的第一列称为第一层 (first layer),这一层的感知器接受三个输入 (evidence) 来决定输出。Perceptrons 的第二层,则以第一层的输出结果作为输入来产生最后的输出,因此第二层可以认为是在处理比第一层更加复杂抽象的工作。
为了简化数学表达,我们将 \(\sum\_{j}{w\_jx\_j}\) 表示成 \(WX\),\(W\)、\(X\) 分别代表权重和输入的向量。同时,我们将阈值的负值 (-threshold) 表示成 bias,即 \(b = -threshold\)。这样,Perceptrons 的输出可以重写为: \[ output=\begin{cases} 0 &if \ \ WX+b <= 0 \\\\ 1 &if \ \ WX+b > 0 \end{cases}. \]
Sigmoid neurons
现在,我们考虑一下如何训练 Perceptrons 的参数(W 和 b)。假设网络的参数发生了一点点微小的变化,为了训练过程的可控,网络的输出也应该发生微小的变化。
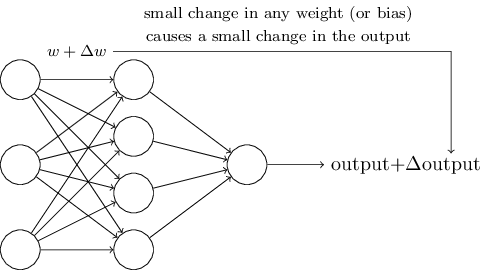
如果网络错误地将手写数字 8 分类为 9,那么我们希望在参数做一点点修改,网络的输出会更靠近 9 这个结果,只要数据量够多,这个修改的过程重复下去,最后网络的输出就会越来越正确,这样神经网络才能不断学习。
然而,对于 Perceptrons 来说,参数的微调却可能导致结果由 0 变为 1,然后导致后面的网络层发生连锁反应。换句话说,Perceptrons 的性质导致它的训练过程是相当难控制的。
为了克服这个问题,我们引入一种新的感知器 sigmoid neuron。它跟 Perceptrons 的结构一模一样,只是在输出结果时加上了一层 sigmoid 函数:\(\sigma(z)=\frac{1}{1+e^{(-z)}}\)。这样,网络的输出就变成了: \[ output=\frac{1}{1+exp(-(WX+b))} \] sigmoid 函数的图像如下:
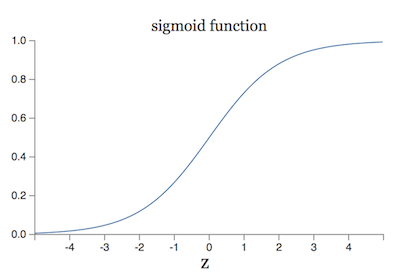
当 \(WX+b\) 趋于 ∞ 的时候,函数值趋于 1,当 \(WX+b\) 趋于 0 的时候,函数值趋于 0。在这种情况下,sigmoid neuron 就退化成 Perceptrons。
sigmoid 函数也可以看作是对 step 函数的平滑,step 函数如下:
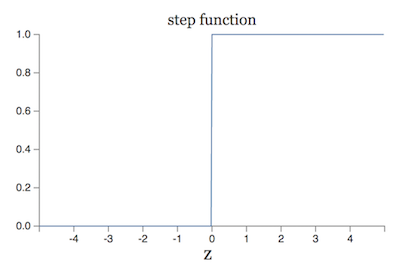
可以看出,Perceptrons neuron 的本质就是 step 函数。
那么,为什么 sigmoid neuron 就比 Perceptrons 更容易训练呢?原因在于,sigmoid 函数是平滑、连续的,它不会发生 step 函数那种从 0 到 1 的突变。用数学的语言表达就是,参数微小的改变(\(\Delta w_j\)、\(\Delta b\))只会引起 output 的微小改变:\(\Delta output \approx \sum_j{\frac{\partial output}{\partial w_j}\Delta w_j}+\frac{\partial output}{\partial b}\Delta b\)。可以发现,\(\Delta output\) 和 \(\Delta w_j\)、\(\Delta b\) 是一个线性关系,这使得网络的训练更加可控。
事实上,正是 sigmoid 函数这种平滑的特性起了关键作用,而函数的具体形式则无关紧要。在本书后面的章节中,还会介绍其他函数来代替 sigmoid,这类函数有个学名叫激活函数 (activation function)。从数学上讲,函数平滑意味着函数在定义域内是可导的,而且导数有很好的数学特性(比如上面提到的线性关系),step 函数虽然分段可导,但它的导数值要么一直是 0,要么在突变点不可导,所以它不具备平滑性。
Learning with gradient descent
假设神经网络的输入是由图片像素组成的一维向量 $x $,输出是一个 one-hot 向量 \(\overline y = y(\overline x)\)。为了量化神经网络的输出结果,我们定义一个代价函数: \[ C(w, b) = \frac{1}{2n}\sum_x||y(x)-a||^2 \tag{6} \] 其中,\(w\) 表示网络的权重参数,\(b\) 表示 biases,\(n\) 是样本数,\(a\) 是网络的输出结果。我们称 \(C\) 为二次代价函数,或者称为平方差(MSE)。当 \(y(x)\) 和 \(a\) 很接近的时候,\(C \approx 0\)。因此,我们的训练算法就是为降低代价函数的值,而最常用的算法就是梯度下降(gradient descent)。
其实我们在高中阶段就遇到过类似的问题:已知函数曲线过几个点,求出这条曲线的方程。不同的是,这里是用代价函数间接求函数参数,而且,这里不是要让函数穿过这些点,而是去拟合、逼近这些点。
现在我们要思考一个问题,为什么要使用平方差作为代价函数?既然我们感兴趣的就是图片被正确分类的数量,那为什么不直接降低这个数量的值,而是绕个弯去降低一个二次代价函数?原因在于图片正确分类的数量这个函数不是一个平滑的函数,换句话说,\(w\) 和 \(b\) 的微小变化对这个函数的影响是不可控的,道理和上面的 sigmoid 函数一样。所以,我们采用这个上面的二次代价函数。
事实上,还有其他平滑的函数可以作为代价函数,这里我们只简单介绍二次代价函数。
讲到这里,我们提到了两次平滑函数:sigmoid 和 二次代价函数。其中,前者是神经网络的输出,后者是对神经网络结果的一种评估,是为了方便对网络参数进行训练。这里要求使用平滑函数是为了使训练的过程更加可控。虽然我们优化的时候是针对代价函数调整参数,但 sigmoid 函数会在代价函数中被使用,所以这两个函数都必须是平滑的。
gradient descent
下面,我们先将这些函数抛在一边,研究一下梯度下降方法。
假设我们要最小化一个函数 \(C(\overline v)\),其中 \(\overline v = v_1, v_2, …\)。
简单起见,我们假设参数是二维的,函数图像长这个样子:
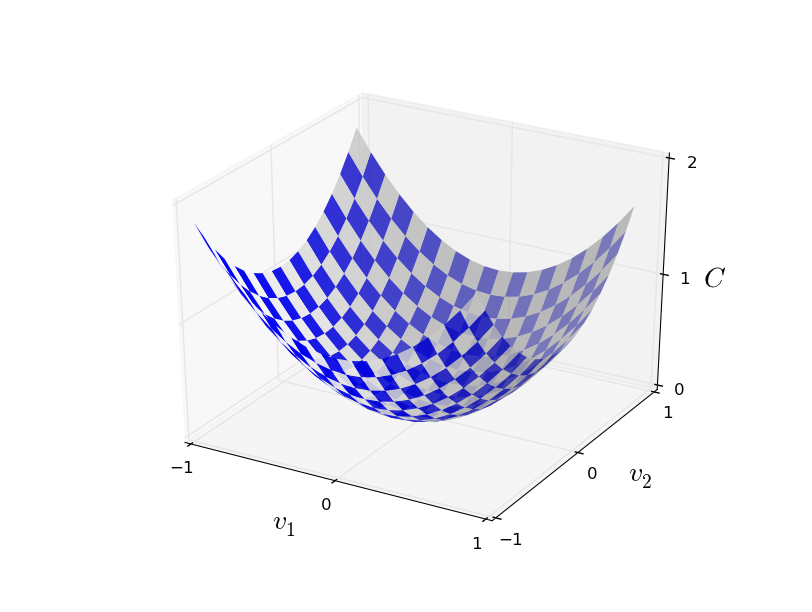
想求这个函数在哪个点取的最小值,数学家们的方法是对函数求导(多个参数就求偏导),然后判断在每一维上的单调性,最后求出在每个维度上的最小值点。这种方法理论上一定可以求出这个函数的最低点,不过,实际上却很难执行,因为函数图像可能会非常复杂,维度可能很高(上图只是一个简单的例子)。
所以,科学家们提出一种看似简单但实际上却屡试不爽的技巧:梯度下降。这种方法的思路是:不管函数图像是什么样的,反正我只往函数每一维度的梯度方向前进。所谓函数梯度,其实就是函数的导数方向:\(\nabla C=(\frac{\partial C}{\partial {v_1}}, \frac{\partial C}{\partial {v_2}})^T\)。然后,我们让函数参数也往这个方向移动:\(v → v' = v + \Delta v = v -\eta \nabla C\),其中,\(\eta\) 称为学习率,\(\Delta v\) 称为步长。这样,函数每次的偏移量为 \(\Delta C \approx \nabla C \Delta v = \frac{\partial C}{\partial v_1} \Delta v_1 + \frac{\partial C}{\partial v_2} \Delta v_2\)。不管函数导数的值是正是负(函数图像向上还是向下),只要学习率适当,这个式子都能保证函数往最低点走,当然,如果学习率的取值过大,函数的下降可能会出现曲折抖动的情况。
梯度下降也存在一些不足之处,比如,如果函数存在多个局部最低值,梯度下降可能会陷入局部最低点出不来。
回到实际问题,现在我们将梯度下降应用到网络参数中: \[ w_k → w_{k}' = w_k-\eta \frac{\partial C}{\partial w_k} \] \[ b_l → b_{l}' = b_l-\eta \frac{\partial C}{\partial b_l} \]
通过不断迭代上面的过程,代价函数会不断下降,运气好的话就可能下降到全局最低点的位置。
stochastic gradient descent
不过,这里有个计算上的问题,我们之前的二次代价函数为:\(C(w,b)=\frac{1}{2n}\sum_x ||y(x)-a||^2\),因此,在计算导数的时候,需要将每个样本的导数值都加起来取平均,这在概率学上是有意义的(防止个别噪声样本的影响),但实际计算的时候,由于样本数量很大,这无疑会造成巨大的计算量。因此,有人又提出一种随机梯度下降(stochastic gradient descent)的方法来加快训练。这种方法每次只挑选少量的随机样本进行训练(当然,所有样本在一轮训练中都需要被挑选到)。
具体来说,假设我们每次挑选 m 个随机样本进行训练,总样本数为 n,那么,只要 m 足够大,我们可以得到一个近似关系(大数定理?): \[ \frac{\sum_{j=1}^{m}\Delta C_{X_{j}}}{m} \approx \frac{\sum_{x} \Delta C_x}{n} = \Delta C \tag{18} \] 然后,每次对参数的训练就变成: \[ w_k→w_{k}'=w_k-\frac{\eta}{m} \sum_j \frac{\partial C}{\partial w_k} \tag{20} \] \[ b_l→b_l'=b_l-\frac{\eta}{m} \sum_j \frac{\partial C}{\partial b_l} \tag{21} \]
有时候,人们会忽略等式前面的\(\frac{1}{n}\)或\(\frac{1}{m}\),只在单一的样本上进行训练。这种方法在样本事先不知道(例如,样本是实时产生的)的情况下比较有效。