3D中的旋转变换

发表于 | 分类于 |

相比 2D 中的旋转变换，3D 中的旋转变换复杂了很多。关于 2D 空间的旋转，可以看这篇文章。本文主要粗略地探讨一下 3D 空间中的旋转。

旋转的要素

所谓旋转要素就是说，我们只有知道了这些条件，才知道怎么旋转一个物体。回忆 2D 空间中的旋转，我们需要确定旋转中心、旋转角以及旋转方向才能旋转一个图形。以此类推，到了 3D 空间，我们仍然需要确定三个要素：一个旋转轴、旋转角以及旋转方向。 下面，为了讲解的方便，旋转方向默认为：正对旋转轴正方向，按逆时针方向为旋转正方向，反之为旋转负方向。

旋转的几种情况

3D 中的旋转本质上可以分为下面三类情况： 1. 绕 x / y / z 轴旋转； 2. 绕通过原点的直线旋转； 3. 绕不通过原点的直线旋转。

可能有同学不理解为什么要分这么多情况讨论，其实这是一个将复杂的问题简单化的过程。在旋转 2D 空间中的物体时，我们也只是计算出绕原点旋转的公式，然后将旋转点平移到跟原点重合，再根据公式旋转物体，最后再平移回去。其实完全可以计算出一个绕任意轴旋转的通用公式，但那样会导致计算量更大。

绕 x / y / z 轴旋转

这是最简单的旋转情况，只要把 2D 中的旋转延伸到 3D 空间就可以了。

绕 x 轴旋转

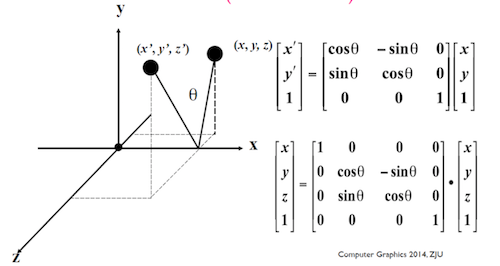rotate-x-axis 上图是一个绕 x 轴旋转的图示。假设我们需要从点(\(x, y, z\))绕 x 轴旋转 \(\theta\) 角到点 (\(x^{'}, y^{'}, z^{'}\))，那么，旋转过程中，x 的坐标值始终都是固定不变的，因此，我们可以把它当作是在\(x=x^{'}\)这个平面上进行旋转，从而退化成一个 2D 旋转的问题。 上图右边的两个矩阵，上面那个是 2D 旋转矩阵，而底下那个只是把该矩阵延伸到 3D 空间而已（为了将平移也纳入矩阵运算，3D 的变换都是采用齐次坐标）。因为 x 轴是旋转轴，因此实际上是在 yoz 平面上做 2D 旋转。只要你知道 2D 空间那个旋转矩阵怎么计算，3D 的变换只是依葫芦画瓢而已。

绕 y 轴旋转

同理，这里不再赘述。 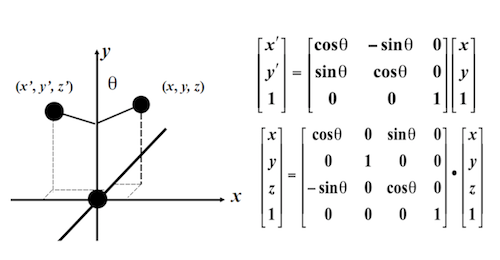rotate-y-axis

绕 z 轴旋转

同理，这里不再赘述。 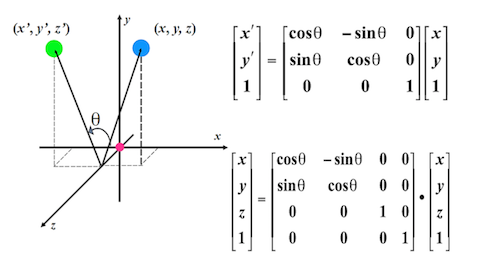rotate-z-axis

绕通过原点的直线旋转

以下所引用的例子来自文末链接三维空间中的旋转：旋转矩阵、欧拉角

现在，假设我们要绕旋转轴 \(P\) 旋转 \(\theta\) 角（如下图所示），那又该如何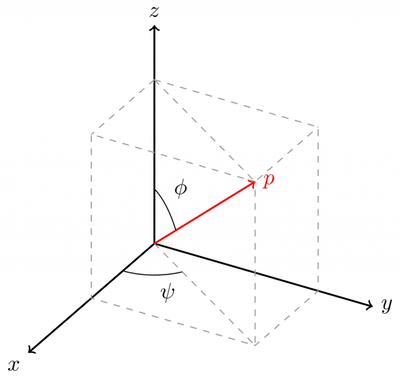？ 3d-angle-rotation 目前我们已有的工具只是绕 x / y / z 轴旋转的矩阵而已。回想 2D 中绕任意点旋转的情况，我们是将任意点变换到原点，绕原点旋转后，再变换回原来的位置。所以，同样的道理，这次我们也将绕 \(P\) 轴的旋转分解为三步（跟原文例子的解释稍有不同，但本质上是一样的）:

  • 将 \(P\) 轴旋转到与 z 轴重合，此时物体跟着旋转到新位置；
  • 让物体绕 z 轴旋转 \(\theta\) 角（可以直接套用之前的矩阵）；
  • 将物体逆向旋转回原来的位置。

下面就针对这三步，解释一下具体的操作。

(1) 首先是将旋转轴旋转到与 z 轴重合。为此，我们需要将 \(P\) 轴绕 z 轴旋转 \(\psi\) 角（根据前面的声明，这里是正方向）。因此，需要乘以矩阵： \[ R_z(\psi)=\begin{bmatrix} cos\psi & -sin\psi & 0 & 0 \\ sin\psi & cos\psi & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \] 旋转完后，\(P\) 轴落入 xoz 平面，然后，按照同样的思路，绕 y 轴旋转 \(\phi\) 角，再乘以矩阵： \[ R_y(\phi)=\begin{bmatrix} cos\phi & 0 & -sin\phi & 0 \\ 0 & 1 & 0 & 0 \\ sin\phi & 0 & cos\phi & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \] 这时，\(P\) 轴与 z 轴已经重合了。

(2) 然后我们让物体绕 z 轴旋转 \(\theta\) 角： \[ R_z(\theta)=\begin{bmatrix} cos\theta & -sin\theta & 0 & 0 \\ sin\theta & cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \] (3) 最后，将物体旋转回之前的位置。具体做法是乘以之前矩阵的逆矩阵。至此，我们得到物体旋转所需要的最终矩阵： \[ R(\theta)=R_z(-\psi)R_y(-\phi)R_z(\theta)R_y(\phi)R_z(\psi) \] 利用旋转矩阵的性质：\(R(-\alpha)=R^{-1}(\alpha)=R^T(\alpha)\)，我们也可以写成： \[ R(\theta)=R_z^T(\psi)R_y^T(\phi)R_z(\theta)R_y(\phi)R_z(\psi) \]

绕不通过原点的直线旋转

有了上面的基础作铺垫，这种情况将变得十分简单。只要将旋转轴平移到经过原点的位置，那么问题就转换成上面的情况，最后再平移回去就可以了。因此，变换矩阵只是在上一种情况的基础上，乘上平移矩阵： \[ R(\theta)=T(x_1, y_1, z_1)R_z^T(\psi)R_y^T(\phi)R_z(\theta)R_y(\phi)R_z(\psi)T(-x_1, -y_1, -z_1) \]

参考

  1. Interactive Computer Graphics - A Top-Down Approach 6e By Edward Angel and Dave Shreiner (Pearson, 2012)
  2. 三维空间中的旋转：旋转矩阵、欧拉角