缩放操作
缩放无非就是放大和缩小两种,不管是哪种操作,都可以得到长宽各自缩放的比值。得到的新图要么是像素增加了(拉长),要么是像素减少了(缩短)。不管是哪种情况,都需要对新图中的像素值赋值(也叫插值)。本文只介绍一下最常见的最邻近插值和双线性插值。
什么是插值
首先讲讲什么叫插值。简单地说,给缩放后得到的新图的每一个像素点赋值,就叫做插值。最常见的插值方法分两种:
一、向前映射:遍历原图中的每一个像素点,根据映射关系可以计算出它们在新图中的位置(遇到小数的情况要取整),这个新位置可以直接取原图对应点的像素值,也可以取一个接近的值。这种方法可能导致新图中存在空洞点,即原图中的所有像素点都无法映射到这个位置点,另一个缺陷是,原图中两个不同的像素点可能映射到同一个位置,这样肯定会有一个像素的信息丢失了;
二、向后映射:这里我们是反过来求出新图到原图的映射变换(按照线性代数的知识,就是将向前映射取一个逆),然后遍历新图中的每个像素,计算出它们在原图中的对应位置,再取值。同样的,这个位置可能不是整数,简单的做法可以直接取整,比较好的做法是综合一下周围点的像素值取一个均值。前一种做法称为最邻近插值,后一种做法根据综合像素的方式又分为几种方法,这里只讲最常见的双线性插值。
最邻近插值
我们就拿一个方向的缩放为例。
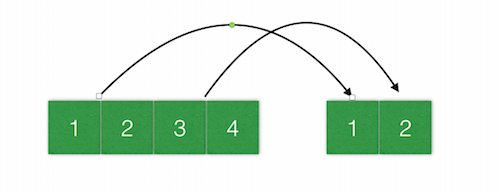
假设右边两个像素点的图是原图,左边四个像素点的图是新图,对于这种宽度扩大两倍,高度保持不变的情况,最邻近插值的做法是这样:我们先计算出新图回到原图的缩放因子是 0.5,所以,对新图中的每个像素,我们计算出它们乘以 0.5 后得到的位置,这个位置是它们对应于原图的位置。新图中,1、2 像素点的位置分别为 (0,0)、(0,1),缩小后得到的新位置为 (0,0),也就是它们对应原图中的 1 像素点,所以它们的像素值都取原图中 1 像素点的值,同理,3、4 像素点的值取原图中 2 像素点的值。这样,新图的像素肯定能被插满。对于原图缩小的情况道理是一样的。
这种做法的优点是简单粗暴,计算量小且容易理解,缺点是由于太过简单粗暴,导致没有很好的利用原图的信息,比方说上图,原图被拉长后,1 和 2 之间的像素应该要有一个过渡,这样人眼看的时候才不会觉得突兀(或者说变化太快),图像中常见的锯齿就是这种由突兀产生的。
上一段简单的代码,用到了 CImg 库(太简单不解释):
1 | CImg<unsigned char> nearest_scale(const CImg<unsigned char>& srcImg, |
双线性插值
既然有双线性插值,我们不妨先看下单线性插值。
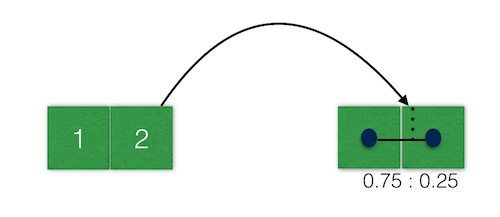
上图中,我们一样假设右图为原图,左图为缩放后的新图。我们通过计算缩放因子,发现左图中 2 这个像素点还原到新图后,对应的坐标不是整数,它恰好落在原图两个像素点之间 0.75 : 0.25 的位置(注意最邻近插值有个取整操作,把位置上的这点细节忽略了)。此时,为了更好地取值,我们不是简单粗暴地用原图中的一个像素值去取代新图,而是根据距离的比值取了一个综合的结果。线性插值的做法是,根据距离比 0.75 : 0.25,对原像素值取一个加权平均,距离近的,像素值要接近,所以权值更大,应该取 0.75,距离远的则相反,取 0.25,这样一来,原图中的两个像素值,根据距离的反比取一个加权平均,就是新图中 2 这个像素的值了。双线性插值道理同上,只不过推广到二维的情况:
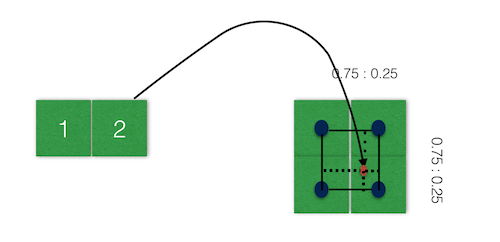
除了水平方向,我们发现高度其实也不是整数,双线性插值会进一步再考虑高度的距离比,假设宽度的距离比是 u : (1-u),高度的距离比是 v : (1-v),此时,我们要综合考虑周围四个点的情况,比方说,对于原图右下角的像素值,对应的加权值为 (1-0.25)*(1-0.25),而右上角的像素值,对应的加权值为 (1-0.75)*(1-0.25),左边的类似,最后将这些值全部加起来就是新的像素值了。
示例代码:
1 | CImg<unsigned char> bilinear_scale(const CImg<unsigned char>& srcImg, |
旋转操作
旋转跟缩放本质上是一样的,只是映射变换不同。
先看看映射函数怎么求。
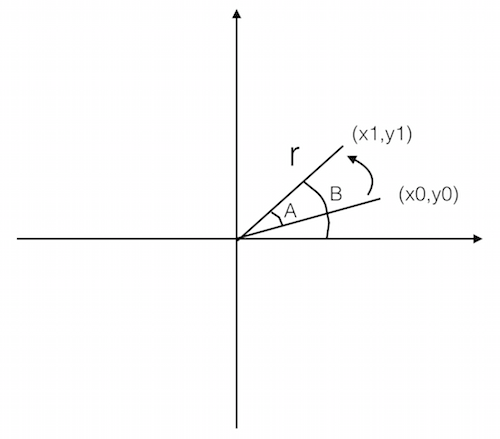
假设点 (\(x_0\), \(y_0\)) 逆时针旋转到 (\(x_1\), \(y_1\)) 的位置,旋转角度为 A,(\(x_1\), \(y_1\)) 与 x 轴正方向的夹角为 B,且知道点 (\(x_0\), \(y_0\)) 到原点的距离为 r (这个量只是起到中间变量的作用)。现在需要求出 \(x_0\),\(y_0\),\(x_1\),\(y_1\) 之间的映射关系。
根据高中三角函数的知识,可以列出如下等式: \[x_0=r cos(B-A)=rcosBcosA+rsinBsinA \tag{1}\] \[y_0=r sin(B-A)=r sinBcosA-rsinAcosB \tag{2}\] \[x_1=r cosB \tag{3}\] \[y_1=r sinB \tag{4}\] 将 (3) (4) 式分别代入 (1) (2) 得到: \[x_0 = x_1 cosA + y_1 sinA \tag{5} \] \[y_0=y_1cosA-x_1sinA \tag{6} \] 这样,向后映射的表达式我们就求出来了。
接着,由 (5) (6) 式分别可得: \[y_1=\frac{x_0-x_1cosA}{sinA} \tag{7}\] \[y_1=\frac{y_0+x_1sinA}{cosA} \tag{8}\] 再由 (7) = (8) 可以解出: \[ x_1=x_0*cosA-y_0*sinA \] 同样的方法可以解出: \[ y_1=y_0*cosA+x_0*sinA \] 这样,向前映射也得到了。之后,按照缩放里面的思路,我们只要先算出新图的大小(根据向前映射可以求得),然后遍历新图里的像素,根据向后映射反推在原图中的像素位置,再用插值的方法就可以给每个像素点赋值了。要注意的一点是,我们这里是以原点为旋转中心计算出来的表达式,如果直接套用上面的计算结果,那么你得到的新图像是原图绕左上角的点旋转A度角后得到的图(旋转方向取决于 A 的符号)。这是因为计算机中,图片的坐标原点在左上角。如果要让图片让自己的中心旋转,必须先将图片的中心与左上角原点对齐(只需做一下平移即可),旋转完成之后,再按照之前平移的距离方向重新调整位置。
示例代码(采用双线性插值):
1 | /* |
最后放上最邻近插值和双线性插值的旋转效果图,可以看到最邻近插值的锯齿略多于双线性插值
(原图)

(最邻近插值)

(双线性插值)
