需求
SVG 标准指令中的 C/c 可以用于构造三次贝塞尔曲线(cube bezier curve),具体用法是:X0, Y0 C X1 Y1, X2 Y2, X3 Y3,这里面的 X、Y 用的是绝对坐标,它们代表三次贝塞尔曲线的控制点( X0, Y0 和 X3、Y3 恰好是曲线前后端点,所以实际上只有两个控制点)。但我的目的是想对贝塞尔曲线做一次 wrap,而这些控制点并不一定就在曲线上,所以必须先把曲线求出来,再对曲线做 wrap 形变。
准备条件
首先,总得先知道贝塞尔曲线是什么吧~~,这里推荐一篇扫盲文章贝塞尔曲线扫盲,重点要知道曲线中的那些比例关系。其次,既然我们是要从 SVG 的控制点来获得贝塞尔曲线,那总得知道 SVG 是什么以及它的标准语法,这里再推荐一篇深度好文深度掌握SVG路径path的贝塞尔曲线指令,重点是要了解 SVG 中的 path 以及 C/c 相关的指令的用法,还有相对位置等一些概念。
解决方案
好了,既然已经知道贝塞尔曲线以及 SVG 是什么东西了,那么想要自己绘制贝塞尔曲线(曲线要画的多好取决于 wrap 的要求),我们得先拿到控制点(本文只针对 SVG 中的 C/c 指令,也就是三次贝塞尔曲线)。思路就很清晰了:先解析 SVG 的 path,拿到控制点,然后根据控制点绘制曲线,done。
step1:如何根据控制点绘制贝塞尔曲线
先搞定这个大头~~。其实只要了解贝塞尔曲线的概念以及它是怎么画出来的,我发现这其实是个小头。我稍微看了下这篇文章贝塞尔曲线原理(简单阐述),用仅存的一点高中向量知识就画出来了。这里把我看上文时的思考结果记录一下(以下贝塞尔曲线相关的图皆取自上文)。
我们先看看二次贝塞尔曲线怎么画的(所谓二次就是除了前后端点外,只有一个控制点的情况)。
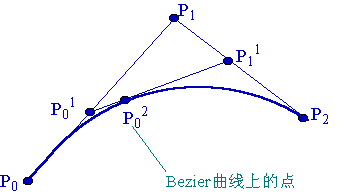
(注意,上面所标点中,右上角的数字不是幂指数,而表示第几次取点),对于二次贝塞尔曲线,我们的目标就是求出一连串的 $P_{0}^2 $,这些 \(P_{0}^2\) 最终构成我们的贝塞尔曲线,当然,对于计算机这种离散化的工具,点要取得多密集取决于你自己的要求。下面,要灵活运用比例关系以及向量工具了: \[ \frac{|\overline {P_{0} P_{0}^1}|}{|\overline{P_{0}P_{1}}|}=\frac{|\overline {P_{1} P_{1}^1}|}{|\overline {P_{1}P_{2}}|}=\frac{|\overline {P_{0}^1 P_{0}^2}|}{|\overline {P_{0}^1P_{1}^1}|}=\frac{t}{1} \ \ \ ( t\in [0, 1]) \] 上式中的 || 表示向量的模,因为我印象中向量好像是不能直接相比的,会涉及到方向问题,但在本例中,相比的向量方向都是一致的,所以我们可以把 || 去掉: \[ \frac{\overline {P_{0} P_{0}^1}}{\overline{P_{0}P_{1}}}=\frac{\overline {P_{1} P_{1}^1}}{\overline {P_{1}P_{2}}}=\frac{\overline {P_{0}^1 P_{0}^2}}{\overline {P_{0}^1P_{1}^1}}=\frac{t}{1} \ \ \ (t\in [0, 1]) \] 然后改变一下分母(结合图像): \[ \frac{\overline {P_{0} P_{0}^1}}{\overline{P_{0}^1P_{1}}}=\frac{\overline {P_{1} P_{1}^1}}{\overline {P_{1}^1P_{2}}}=\frac{\overline {P_{0}^1 P_{0}^2}}{\overline {P_{0}^2P_{1}^1}}=\frac{t}{1-t} \ \ \ (t\in [0, 1]) \] 下一步,求出 \(\overline {p_{0}^1}\),由上式可得: \[ (1-t)\overline{P_{0}P_{0}^1}=t\overline{P_{0}^1P_{1}} \\\\ (1-t)(\bar{P_{0}^1}-\bar{P_{1}})=t(\bar{P_{1}}-\bar{P_{0}}) \] 注意这一步开始将向量拆成两个向量相减的形式,这样后者中的向量我们可以直接用坐标表示了(比如:\(\bar P_{0}\) 就表示 \(\bar P_{0}\) 这个点本身的坐标)。将上式化简得到: \[ \overline {P_{0}^1} = (1-t)\overline{P_{0}}+t\overline{P_{1}} \tag{1} \] 同样的方法求解出 \(\overline{P_{1}^1}\) 和 \(\overline{P_{0}^2}\): \[ \overline {P_{1}^1} = (1-t)\overline{P_1}+t\overline{P_2} \tag{2} \] \[ \overline{P_0^2}=(1-t)\overline{P_0^1}+t\overline{P_1^1} \tag{3} \]
将 (1)(2) 式代入 (3) 式并化简可得: \[ \overline{P_{0}^2}=(1-t)^2 \overline{P_{0}} + 2t(1-t) \overline{P_{1}} + t^2 \overline{P_{2}} \] 如果耐心看到这一步,那么二次贝塞尔曲线就应该会画了,因为三个点的坐标已知,需要做的就是改变 t 的值来重复得到 \(\overline{P_{0}^2}\) 的坐标,这个 t 的值在 [0,1] 之间变化,变化的间隔决定了曲线点的疏密程度,下面是计算二次贝塞尔曲线的代码片段,用了「CImg」库,t 的间隔取 0.01,参照上面的计算结果很快就明白了:
1 | void draw_quad_bezier(CImg<unsigned char> &img, Point p0, Point p1, Point p2) { |
效果图如下(三个点的坐标分别取 (100,100),(500,1000),(1500,200) ):

好了,二次的我们会求了,那三次的怎么求呢?道理是一样的,不然前面码那么多公式不就浪费了嘛^_^
观察一下三次贝塞尔曲线的图:
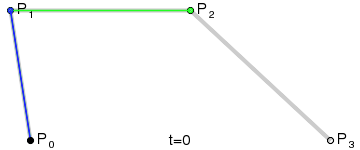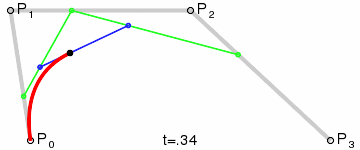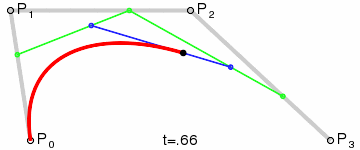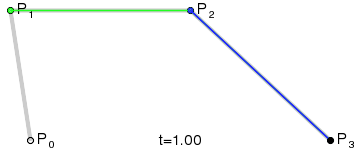
你会发现,原来它就是在原来二次曲线的三个控制点外围又套了一层,也就是说,我们要先通过三次贝塞尔曲线的四个控制点,求出绿色那一条线的三个端点,再把这三个端点代入之前求出来的二次曲线的公式即可。道理就是这么简单,所以我也懒得码公式了,直接上一幅我的草稿图(纯粹给自己以后看的=.=):


最后得出来的计算结果: \[ \overline{P_{0}^3}=(1-t)^3 \overline{P_{0}}+3t(1-t)^2 \overline{P_{1}}+3t^2(1-t) \overline{P_{2}}+t^3 \overline{P_{3}} \] 来,照例给出代码片段:
1 | void draw_cube_bezier(CImg<unsigned char> &img, Point p0, Point p1, Point p2, Point p3) { |
效果图如下

这样一来,三次贝塞尔曲线的绘制部分基本结束了。不过,虽然我们的目标是绘制三次贝塞尔曲线,也就是输入四个点输出一条曲线的情况,可如果遇到输入的点退化成三个的情况,我们的方法是否适用呢?(鉴于我的项目,这里主要指四个控制点中有两个控制点相同的情况,也就是起码有三个点不同,而且输入的控制点数量一定是 4 个)。
没有具体去证明,稍微假设我们上面得到的三次曲线的最终表达式中,\(\overline{P_{0}}\) 和 \(\overline{P_{1}}\) 相同,那么最终结果跟二次曲线的表达式还是有较大不同的,但实际操作时发现,这种不同在人眼可以忍受的误差范围内,下面是我尝试的一个例子:
二次贝塞尔曲线,输入点分别为:(100,100), (500,1000), (1500,200)

三次贝塞尔曲线,输入点分别为:(100,100), (100,100), (500,1000), (1500,200),即前两个点一样

可以看出形状上基本一样,也就是说,对于退化的情况,我们的算法基本可以得到一致的二次贝塞尔曲线。而且真实项目中,贝塞尔曲线的控制点都靠的比较近,因此人眼基本看不出区别,所以这里不再进一步细化算法。
step2: 如何提取控制点
要提取的 svg 中的控制点位于 path 标签内,大致如下:
1 | <svg xmlns="http://www.w3.org/2000/svg" width="450px" height="600px" |
浏览器中显示的是一张人脸图:
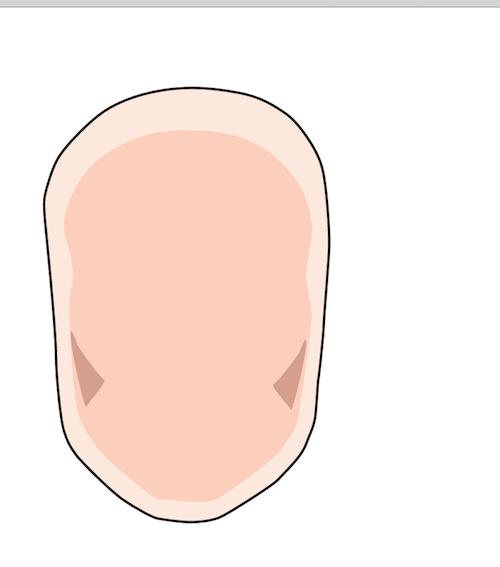
当然我要提取的只是最外层的脸轮廓。
虽然有些素材的路径不太一致,但大部分素材的格式还是很接近的,所以我的想法是用字符串分割的方式把绝大部分素材的控制点都提取出来,对于比较特殊的素材,要么放弃,要么手动修改 svg,或者微调一下算法都可以。然而就是这看似简单的一步让我颓废了一个下午。原因不是 svg 的解析,也不是字符串的切割,而是控制点的还原。注意到上面的 svg 中,贝塞尔曲线用的是 c 指令,也就是相对位置,但我之前的算法要求使用绝对位置。于是,我的做法是:每隔四个点取一段,其中每段的最后一个点作为下一段的起点,在取的过程中,根据相对位置重新计算出点的绝对位置。这里的坑就在计算绝对位置这一步。我看了 w3school 和 mozilla 上的教程,说的都是:相对于上一个点的坐标,根据相对位置计算出下一个点的坐标,于是我简单地写了一个循环
1 | for (int i = 1; i < points.size(); i++) { |
但结果中,我惊异地发现出现了坐标值为负数的情况,反复检查后,发现问题只可能出现在计算绝对位置这一步,然后就是不停地 goolging,连百度都用上了,但是居然没查到类似的问题(当然可能是我查问题的姿势不对,不过当时怎么就没想到去查 SVG 的官方资料呢,看来还是懒=。=)。然后我又怀疑是不是浏览器内部对点的坐标做了归一化处理,也就是对越界的点做了平移。于是就把我的计算结果扔到 chrome 里面,结果很欣慰的,脸消失了一部分,那问题只可能是坐标计算错了。第二天,我就在 StackOverflow 上发了处女帖,Draw Bezier Curve with relative path in SVG,吃顿饭的功夫就收到了答复。在这里不得不佩服国外程序员(也可能是天朝的?)的 manner,让我这种平时只找答案不回答的人即感动又内疚。原来,对于贝塞尔曲线而言,相对位置的坐标是以上一段曲线或直线的终点,也就是本段贝塞尔曲线的起点为标准的,所以应该把代码改为:
1 | int lastEndPoint = 0; |
然后我终于成功地画出一张人脸(右边为浏览器中的对照结果): 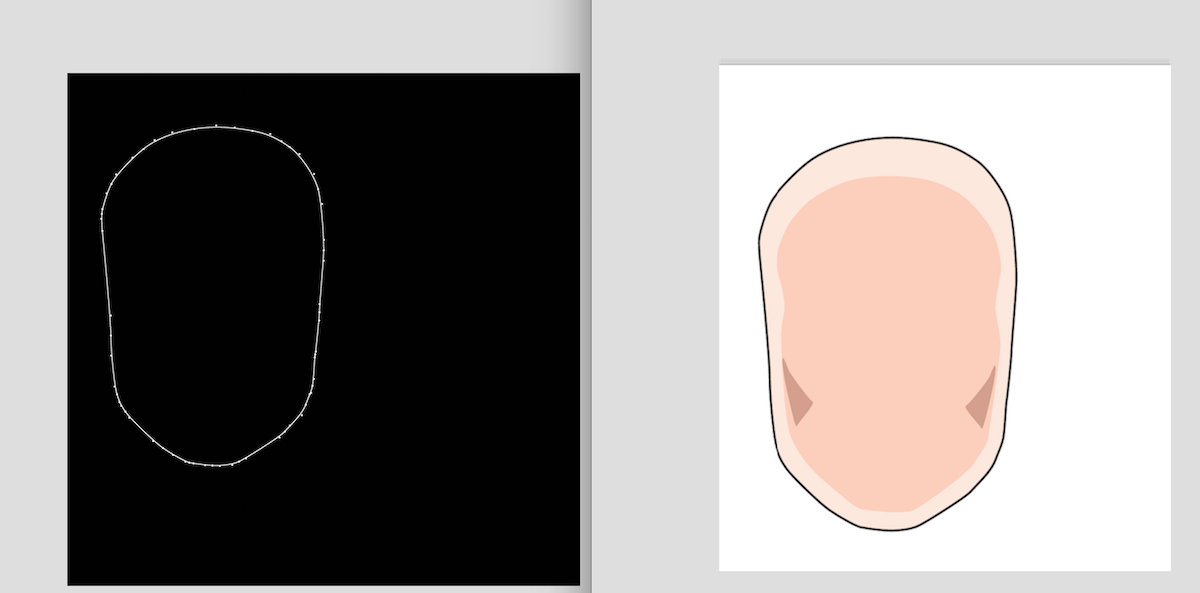
仔细一看我发现,好像素材中的控制点也基本在贝塞尔曲线上啊,这样直接拿控制点做形变误差应该也不会差很多才对😂。然而都已经把曲线画出来了。。。。。。
参考
还有一篇我提问的SO😢:Draw Bezier Curve with relative path in SVG