绘制三角形

其实这应该属于图像处理的入门内容，因为跟三角形相关所以 mark 一下。

需求

我们要实现这样一个函数，输入参数是绘制的图片以及三角形三个点：

1	function(image, point1, point2, point3)

简单起见，不考虑输入的点超过图片范围等异常情况，假设输入都合法，并且输入图片是像素全为 0 的黑图。任务是将三个点构成的区域像素值设为 255，即白色。

准备条件

图像读取采用 Cimg 这个轻量级的库，编程语言采用 C++。

思路

绘制方法无非是遍历图片中的每个像素，判断该像素是否落在三角形内，是的话将像素值设为 255。那么重点便是如何判断一个像素是否在三角形内。这里参考了这篇文章中的第二种方法：Point in triangle test 。稍微讲解如下：

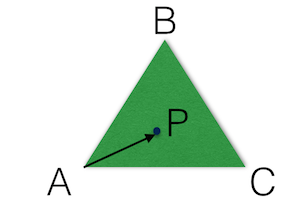
假设我们的三角形长这样，现在要让程序判断 P 点是否在三角形内。这里要用到一点高中向量的知识。假设 A、B、C 三点坐标分别为 (x1, y1)，(x2, y2)，(x3, y3)，P 点坐标是 (x, y)。根据向量知识，有这样一个等式：[PA]=u*[BA]+v*[CA] (这里的[]表示一个向量，不知道怎么用 md 表示向量，先将就一下)，如果 u+v<=1 && u>=0 && v>=0 ，那么 P 就在三角形中，否则 P 在三角形外。因为 A、B、C、P 的坐标都是知道的，只要解出 u 和 v，就能判断出这个 P 点坐标的情况。那么如何求出这两个值呢？其实方法也非常简单，我们先把之前公式里的向量用坐标的形式表示，可以得出 [x-x1, y-y1]=u*[x2-x1, y2-y1]+v*[x3-x1, y3-y1] ，而后将 x、y 分离得到两个等式：x-x1=u*(x2-x1)+v*(x3-x1) 、y-y1=u*(y2-y1)+v*(y3-y1) ，两个方程两个未知数，可以求出： \[ u=\frac{(y-y1)(x3-x1)-(x-x1)(y3-y1)}{(y2-y1)(x3-x1)-(x2-x1)(y3-y1)} \]

\[ v=\frac{(y-y1)(x2-x1)-(x-x1)(y2-y1)}{(y3-y1)(x2-x1)-(x3-x1)(y2-y1)} \]

(可能有老眼昏花算错的地方)

代码

简单把上面的思路翻译一下就是代码了

void draw_triangle(CImg<unsigned char>& srcImg, int x1, int y1, 
	int x2, int y2, int x3, int y3) {
    int width = srcImg.width();
    int height = srcImg.height();
    for (int i = 0; i < width; i++) {
      for (int j = 0; j < height; j++) {
        double vx1 = x2 - x1, vy1 = y2 - y1, vx2 = x3 - x1, vy2 = y3 - y1;
        double vx0 = i - x1, vy0 = j - y1;
        double u = (vx2*vy0 - vx0*vy2) / (double)(vx2*vy1 - vx1*vy2),
        v = (vx1*vy0 - vx0*vy1) / (double)(vx1*vy2 - vx2*vy1);
        if (u >= 0 && v >= 0 && u+v <= 1) {
          for (int channel = 0; channel < 3; channel++) {
            srcImg(i, j, 0, channel) = 0;
          }
        }
      }
    }
	
}

缺陷：

这种方法计算量不算大，但由于使用了除法，可能出现除数为 0 的情况（讲道理应该不可能，u、v 的值应该不会无穷大才对，不知道是否有前辈已经证明）。

参考：

Point in triangle test