上一篇文章介绍了矩阵量化的基本原理,并推广到卷积网络中。这一章开始,我会逐步深入到卷积网络的量化细节中,并用 pytorch 从零搭建一个量化模型,帮助读者实际感受量化的具体流程。
本章中,我们来具体学习最简单的量化方法——后训练量化「post training quantization」
卷积层量化
卷积网络最核心的要素是卷积,前文虽然有提及卷积运算的量化,但省略了很多细节,本文继续深入卷积层的量化。
这里我们继续沿用之前的公式,用 \(S\)、\(Z\) 表示 scale 和 zero point,\(r\) 表示浮点实数,\(q\) 表示定点整数。
假设卷积的权重 weight 为 \(w\),bias 为 \(b\),输入为 \(x\),输出的激活值为 \(a\)。由于卷积本质上就是矩阵运算,因此可以表示成: \[ a=\sum_{i}^N w_i x_i+b \tag{1} \] 由此得到量化的公式: \[ S_a (q_a-Z_a)=\sum_{i}^N S_w(q_w-Z_w)S_x(q_x-Z_x)+S_b(q_b-Z_b) \tag{2} \]
\[ q_a=\frac{S_w S_x}{S_a}\sum_{i}^N (q_w-Z_w)(q_x-Z_x)+\frac{S_b}{S_a}(q_b-Z_b)+Z_a \tag{3} \]
这里面非整数的部分就只有 \(\frac{S_w S_x}{S_a}\)、\(\frac{S_b}{S_a}\),因此接下来就是把这部分也变成定点运算。
对于 bias,由于 \(\sum_{i}^N (q_w-Z_w)(q_x-Z_x)\) 的结果通常会用 int32 的整数存储,因此 bias 通常也量化到 int32。这里我们可以直接用 \(S_w S_x\) 来代替 \(S_b\),由于 \(S_w\)、\(S_x\) 都是对应 8 个 bit 的缩放比例,因此 \(S_w S_x\) 最多就放缩到 16 个 bit,用 32bit 来存放 bias 绰绰有余,而 \(Z_b\) 则直接记为 0。
因此,公式 (3) 再次调整为: \[ \begin{align} q_a&=\frac{S_w S_x}{S_a}(\sum_{i}^N(q_w-Z_w)(q_x-Z_x)+q_b)+Z_a \notag \\ &=M(\sum_{i}^N q_wq_x-\sum_i^N q_wZ_x-\sum_i^N q_xZ_w+\sum_i^NZ_wZ_x+q_b)+Z_a \tag{4} \end{align} \] 其中,\(M=\frac{S_w S_x}{S_a}\)。
根据上一篇文章的介绍,\(M\) 可以通过一个定点小数加上 bit shift 来实现,因此公式 (4) 完全可以通过定点运算进行计算。由于 \(Z_w\)、\(q_w\)、\(Z_x\)、\(q_b\) 都是可以事先计算的,因此 \(\sum_i^N q_wZ_x\)、\(\sum_i^NZ_wZ_x+q_b\) 也可以事先计算好,实际 inference 的时候,只需要计算 \(\sum_{i}^N q_wq_x\) 和 \(\sum_i^N q_xZ_w\) 即可。
卷积网络量化流程
了解完整个卷积层的量化,现在我们再来完整过一遍卷积网络的量化流程。
我们继续沿用前文的小网络:
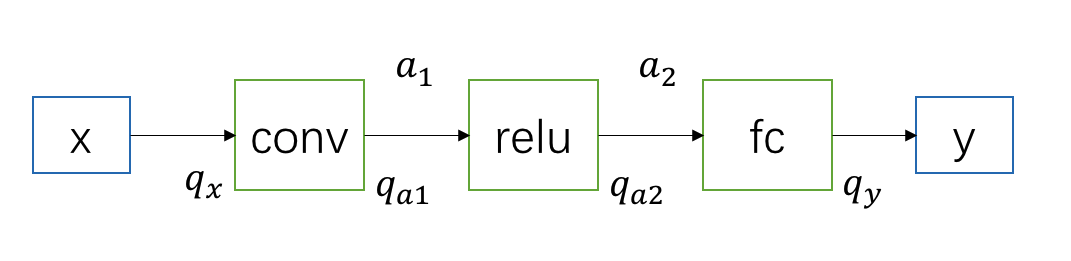
其中,\(x\)、\(y\) 表示输入和输出,\(a_1\)、\(a_2\) 是网络中间的 feature map,\(q_x\) 表示 \(x\) 量化后的定点数,\(q_{a1}\) 等同理。
在后训练量化中,我们需要一些样本来统计 \(x\)、\(a_1\)、\(a_2\) 以及 \(y\) 的数值范围「即 min, max」,再根据量化的位数以及量化方法来计算 scale 和 zero point。
本文中,我们先采用最简单的量化方式,即统计 min、max 后,按照线性量化公式: \[ S = \frac{r_{max}-r_{min}}{q_{max}-q_{min}} \tag{5} \]
\[ Z = round(q_{max} - \frac{r_{max}}{S}) \tag{6} \]
来计算 scale 和 zero point。
需要注意的是,除了第一个 conv 需要统计输入 \(x\) 的 min、max 外,其他层都只需要统计中间输出 feature 的 min、max 即可。另外,对于 relu、maxpooling 这类激活函数来说,它们会沿用上一层输出的 min、max,不需要额外统计,即上图中 \(a_1\)、\(a_2\) 会共享相同的 min、max 「为何这些激活函数可以共享 min max,以及哪些激活函数有这种性质,之后有时间可以细说」。
因此,在最简单的后训练量化算法中,我们会先按照正常的 forward 流程跑一些数据,在这个过程中,统计输入输出以及中间 feature map 的 min、max。等统计得差不多了,我们就可以根据 min、max 来计算 scale 和 zero point,然后根据公式 (4) 对一些数据项提前计算。
之后,在 inference 的时候,我们会先把输入 \(x\) 量化成定点整数 \(q_x\),然后按照公式 (4) 计算卷积的输出 \(q_{a1}\),这个结果依然是整型的,然后继续计算 relu 的输出 \(q_{a2}\)。对于 fc 层来说,它本质上也是矩阵运算,因此也可以用公式 (4) 计算,然后得到 \(q_y\)。最后,根据 fc 层已经计算出来的 scale 和 zero point,推算回浮点实数 \(y\)。除了输入输出的量化和反量化操作,其他流程完全可以用定点运算来完成。
pytorch实现
有了上面的铺垫,现在开始用 pytorch 从零搭建量化模型。
下文的代码都可以在github上找到。
基础量化函数
首先,我们需要把量化的基本公式,也就是公式 (5)(6) 先实现:
1 | def calcScaleZeroPoint(min_val, max_val, num_bits=8): |
前面提到,在后训练量化过程中,需要先统计样本以及中间层的 min、max,同时也频繁涉及到一些量化、反量化操作,因此我们可以把这些功能都封装成一个 QParam 类:
1 | class QParam: |
上面的 update 函数就是用来统计 min、max 的。
量化网络模块
下面要来实现一些最基本网络模块的量化形式,包括 conv、relu、maxpooling 以及 fc 层。
首先我们定义一个量化基类,这样可以减少一些重复代码,也能让代码结构更加清晰:
1 | class QModule(nn.Module): |
这个基类规定了每个量化模块都需要提供的方法。
首先是 __init__ 函数,除了指定量化的位数外,还需指定是否提供量化输入 (qi) 及输出参数 (qo)。在前面也提到,不是每一个网络模块都需要统计输入的 min、max,大部分中间层都是用上一层的 qo 来作为自己的 qi 的,另外有些中间层的激活函数也是直接用上一层的 qi 来作为自己的 qi 和 qo。
其次是 freeze 函数,这个函数会在统计完 min、max 后发挥作用。正如上文所说的,公式 (4) 中有很多项是可以提前计算好的,freeze 就是把这些项提前固定下来,同时也将网络的权重由浮点实数转化为定点整数。
最后是 quantize_inference,这个函数主要是量化 inference 的时候会使用。实际 inference 的时候和正常的 forward 会有一些差异,可以根据之后的代码体会一下。
下面重点看量化卷积层的实现:
1 | class QConv2d(QModule): |
这个类基本涵盖了最精华的部分。
首先是 __init__ 函数,可以看到我传入了一个 conv_module 模块,这个模块对应全精度的卷积层,另外的 qw 参数则是用来统计 weight 的 min、max 以及对 weight 进行量化用的。
其次是 freeze 函数,这个函数主要就是计算公式 (4) 中的 \(M\)、\(q_w\) 以及 \(q_b\)。由于完全实现公式 (4) 的加速效果需要更底层代码的支持,因此在 pytorch 中我用了更简单的实现方式,即优化前的公式 (4): \[
q_a=M(\sum_{i}^N(q_w-Z_w)(q_x-Z_x)+q_b)+Z_a \tag{7}
\] 这里的 \(M\) 本来也需要通过移位来实现定点化加速,但 pytorch 中 bit shift 操作不好实现,因此我们还是用原始的乘法操作来代替。
注意到 freeze 函数可能会传入 qi 或者 qo,这也是之前提到的,有些中间的模块不会有自己的 qi,而是复用之前层的 qo 作为自己的 qi。
接着是 forward 函数,这个函数和正常的 forward 一样,也是在 float 上进行的,只不过需要统计输入输出以及 weight 的 min、max 而已。有读者可能会疑惑为什么需要对 weight 量化到 int8 然后又反量化回 float,这里其实就是所谓的伪量化节点,因为我们在实际量化 inference 的时候会把 weight 量化到 int8,这个过程本身是有精度损失的 (来自四舍五入的 round 带来的截断误差),所以在统计 min、max 的时候,需要把这个过程带来的误差也模拟进去。
最后是 quantize_inference 函数,这个函数在实际 inference 的时候会被调用,对应的就是上面的公式 (7)。注意,这个函数里面的卷积操作是在 int 上进行的,这是量化推理加速的关键「当然,由于 pytorch 的限制,我们仍然是在 float 上计算,只不过数值都是整数。这也可以看出量化推理是跟底层实现紧密结合的技术」。
理解 QConv2d 后,其他模块基本上异曲同工,这里不再赘述。
完整的量化网络
我们定义一个简单的卷积网络:
1 | class Net(nn.Module): |
接下来就是把这个网络的每个模块进行量化,我们单独定义一个 quantize 函数来逐个量化每个模块:
1 | class Net(nn.Module): |
注意,这里只有第一层的 conv 需要 qi,后面的模块基本是复用前面层的 qo 作为当前层的 qi。
接着定义一个 quantize_forward 函数来统计 min、max,同时模拟量化误差:
1 | class Net(nn.Module): |
下面的 freeze 函数会在统计完 min、max 后对一些变量进行固化:
1 | class Net(nn.Module): |
由于我们在量化网络的时候,有些模块是没有定义 qi 的,因此这里需要传入前面层的 qo 作为当前层的 qi。
最后是 quantize_inference 函数,就是实际 inference 的时候用到的函数:
1 | class Net(nn.Module): |
这里我们会将输入 x 先量化到 int8,然后就是全量化的定点运算,得到最后一层的输出后,再反量化回 float 即可。
训练全精度网络
这一部分代码在 train.py 中,我们用 mnist 数据集来训练上面的网络:
1 | device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') |
具体训练细节比较简单,这里不再赘述。
训练完成后,我测试得到的准确率在 98% 左右。
后训练量化
这一部分代码在 post_training_quantize.py 中。
我们先加载全精度模型的参数:
1 | model = Net() |
然后对网络进行量化:
1 | model.quantize(num_bits=8) |
接下来就是用一些训练数据来估计 min、max:
1 | def direct_quantize(model, test_loader): |
简单起见,我们就跑 200 个迭代。
然后,我们把量化参数都固定下来,并进行全量化推理:
1 | model.freeze() |
由于很多细节都封装在量化网络的模块中了,因此外部调用的代码跟全精度模型其实很类似。
我自己测试了 bit 数为 1~8 的准确率,得到下面这张折线图:
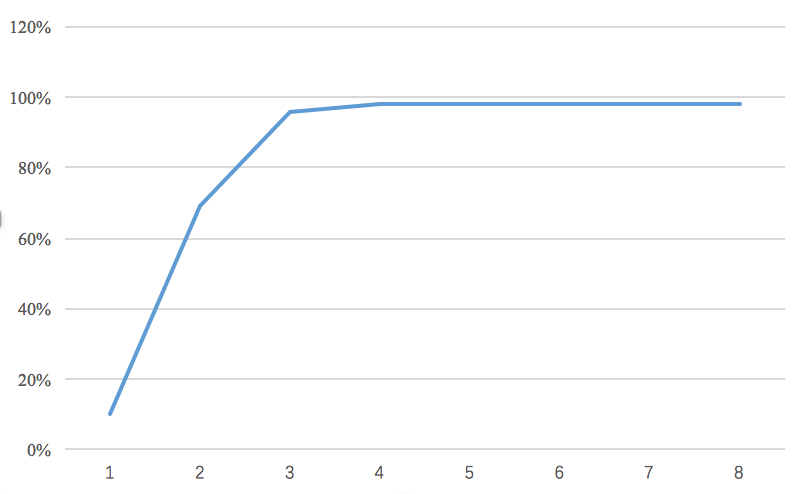
发现,当 bit >= 3 的时候,精度几乎不会掉,bit = 2 的时候精度下降到 69%,bit = 1 的时候则下降到 10%。
这一方面是 mnist 分类任务比较简单,但也说明神经网络中的冗余量其实非常大,所以量化在分类网络中普遍有不错的效果「不过 bit =3 或 4 的时候效果依然这么好,让我依稀觉得代码里面应该有 bug,后续还要反复检查」。
总结
这篇文章主要补充了卷积层量化的细节,包括 bias 的量化,以及实际 inference 时一些优化的操作。并梳理了完整的卷积网络量化的流程。然后重点用 pytorch 从零搭建一个量化模型来帮助大家理解其中的细节,以及后训练量化算法的过程。代码是参考了这篇文章,加上自己拍脑袋构思的,存在很多不足之处,而且应该有不少 bug 存在,也欢迎大家指正。
之后的文章将继续讲述量化感知训练的流程,并补充其他量化的细节「例如 conv+relu 的合并等」,感谢大家赏脸关注。
参考
- How to Quantize an MNIST network to 8 bits in Pytorch from scratch (No retraining required)
- Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference
