我在很久以前的一篇短文提过一丢丢 boosting,今天翻了下统计学习方法,打算记录一点干货的东西。这篇博文会简单介绍一下 「Adaboost」,并总结一下 Adaboost 方法背后的套路:前向分步加法模型。
Adaboost
学过机器学习的同学,想必对 Adaboost 都不会陌生,就算不知道算法原理,也听过算法的名字。正如我之前提到的,Adaboost 采用的思想源于一句古老的俗语「三个臭皮匠,赛过诸葛亮」。不过,与 Bagging 类算法(典型如随机森林)不同的是,Adaboost 希望这三个臭皮匠的分工能逐步提高团队的效益,而不是仅仅起到平等投票的作用。具体到机器学习中,假设我们已经有了几个比较弱的分类器,Adaboost 首先从这些分类器中选出一个分类性能最好的,但这个性能最好的分类器总归有分错的样本,对这些分错的样本,Adaboost 再从剩下的分类器中选一个能把这些样本分得最好的分类器,和刚开始的分类器组合成一个新的分类器,依此类推下去,直到所有弱分类器都组合在一起,成为一个更强的分类器。
算法流程
下面我们用更加数学的语言来表达上面的过程。
假设有一个训练数据集 \(T={(x_1, y_1), (x_2, y_2), … (x_N, y_N)}\),其中 \(x_i \in X \subseteq \mathbf{R^n}\),\(y_i \in Y = {-1, +1}\)(简单起见,假设只有两种分类),并指定一种分类学习算法用于构建弱分类器。接下来我们要用 Adaboost 学习出一个强分类器 \(G(x)\)。
Adaboost 算法流程分为以下几步:
先为每个训练样本初始化一个权值分布: \[ D_1=(w_{1,1},...,w_{1,i},...w_{1,N}), \ w_{1,i}=\frac{1}{N}, \ i=1,2,...,N \] 将 \(G(x)\) 初始化为:\(G_0(x)=0\)。
对 \(m=1,2,…,M\)
根据学习算法,在权值分布为 \(D_m\) 的样本上构建出弱分类器 \(g_m\): \[ e_m=P(g_m(x_i) \neq y_i)=\sum_{i=1}^N w_{m,i}I(g_m(x_i)\neq y_i) \] 这里的 \(I()\) 表示指示函数,当 \(g_m(x_i) \neq y_i\) 时取 1,否则取 0。
计算它的系数: \[ \alpha_m=\frac{1}{2}\log{\frac{1-e_m}{e_m}} \] (这一步要注意,如果 \(e_m\) 都大于 0.5,证明我们已经找不出弱分类器了,这时要么算法停止,要么从头开始)
将得到的分类器加入 \(G(x)\) 中:\(G_m(x)=G_{m-1}(x)+g_m(x)\)。
更新所有训练数据的权值分布: \[ D_{m+1}=(w_{m+1,1},...,w_{m+1,i},...,w_{m+1,N}) \\ w_{m+1,i}=\frac{w_{m,i}}{Z_m}\exp(-\alpha_m y_i G_m(x_i)) \] 这里的 \(Z_m\) 表示规范化因子:\(Z_m=\sum_{i=1}^N{w_{m,i}\exp(-\alpha_m y_i G_m(x_i))}\)。
对这些弱分类器进行线性组合,得到最终的分类器:
\[ G(x)=sign(f(x))=sign(\sum_{m=1}^M \alpha_m G_m(x)) \]
整个算法流程看起来挺复杂的,它是怎么体现之前说的 boosting 的思想的呢?
首先,在计算分类误差率这一步,由于指示函数 \(I()\) 的作用,我们只会挑选出上一步中仍没法正确分对的样本进行判断。在构造出弱分类器后,由于这个弱分类器在这些样本上又能做到 50% 以上的准确率,因此它能使 \(G(x)\) 的总体性能提升一点点。新分类器的权重系数的计算函数为 \(\alpha_m=\frac{1}{2}\log{\frac{1-e_m}{e_m}}\),其图像如下:
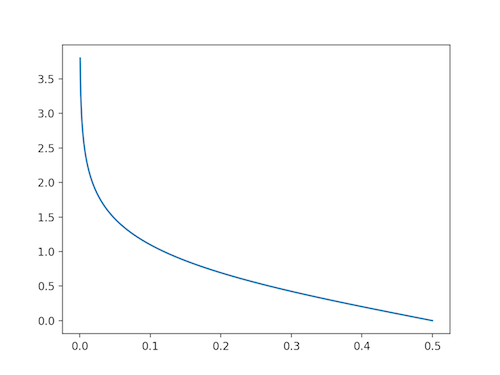
这个函数在 \(e_m > 0.5\) 时会取到负值,由于开始时所有样本的权重均匀,加之弱分类器准确率超过 50%,因此算法开始执行时 \(e_m > 0.5\) 的情况是不会发生的,但随着样本权重的改变,如果之后构造的弱分类器的准确率低于 50%,为了防止分类器权值为负,算法就会终止。如果一个分类器的 \(e_m\) 越小,证明它的错分率越低,效果越好,则它的权重会越大。
每轮计算完弱分类器后,算法会根据公式 \(\frac{w_{m,i}}{Z_m}\exp(-\alpha_m y_i G_m(x_i))\) 更新样本权重,如果这一轮得到的分类器 \(G_m\) 对某个样本的预测错误,证明这个样本仍然是块「硬骨头」,这种情况下,\(\exp(-\alpha_m y_i G_m(x_i))>1\),表示该样本的权重相比上一次而言增大了,这样一来,在下一次构造弱分类器时,该样本会得到更多的关注,而对那些已经正确分类的样本,权重反而会降低。因此,在每轮构造弱分类器的过程中,为了得到更好的分类效果,弱分类器会去挑选那些能把「硬骨头」样本分得更好的特征,所以,Adaboost 在某种程度上来说,具备特征选择的作用。
提升树
提升树也属于一种 boosting 方法,只不过由算法的名字我们也可以推测,这种方法采用的弱分类器是「树」。如果要解决分类问题,可以用决策树,而回归问题则可以用回归树(关于决策树和回归树,可以参考其他资料,或者我之前整理的一篇文章)。
既然是 boosting 方法,那么提升树也和 Adaboost 一样,遵循同样的方法论。如果弱分类器采用的是决策树,那么提升树方法其实等同于弱分类器为决策树的 Adaboost,其算法流程和 Adaboost 一样,所以这里就不再展开讲了。下面分析一下回归问题中提升树的算法原理。
在回归问题中,提升树采用的弱分类器(或者说,弱回归器)是 CART。同样地,假设有一个训练数据集 \(T={(x_1, y_1), (x_2, y_2), … (x_N, y_N)}\),其中,\(x_i \in X \subseteq \mathbf{R^n}\),\(y_i \in Y \subseteq \mathbf{R}\)。