很久以前写过一篇 PCA 的小白教程,不过由于当时对 PCA 的理解流于表面,所以只是介绍了一下 PCA 的算法流程。今天在数图课上偶然听到 PCA 在图像压缩上的应用,突然明白了一点实质性的东西,这里趁热记录一波。

PCA 算法
首先还是简单回顾下 PCA 的算法流程。
我们把样本数据 \(x\) 归一化后,计算其协方差矩阵 \(C_x\),然后计算 \(C_x\) 的特征向量,构造出一个特征向量矩阵 \(A\),最后把 \(x\) 通过该矩阵映射到一个新的空间,得到的向量 \(y\) 就是能体现 \(x\) 主要成分的向量了。
PCA 在做什么
那么,这种空间映射有什么意义呢?问题要回到协方差矩阵 \(C_x\) 上。我们知道,协方差矩阵是一个对称矩阵,在线性代数中,对称矩阵的特征向量是相互正交的。而我们把 \(x\) 通过这个特征向量矩阵映射到 \(y\),其实就是把原来的数据由最初的 \([e_1, e_2, \dots, e_n]\) 的单位坐标系,调整到这些正交的特征向量组成的坐标系下,如下图所示:
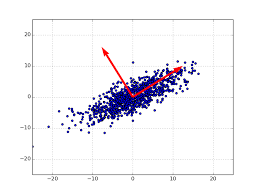
这种坐标变换的意义又在哪呢?
如果仔细分析,我们就会发现,这些新得到的向量 \(y\) 的均值为 \(0\),而且它们的协方差矩阵为: \[ C_y=AC_xA^T=\begin{bmatrix} \lambda_1 & & & 0 \\ & \lambda_2 & & \\ & & \ddots & \\ 0 & & & \lambda_n \end{bmatrix} \] 这里,\(A\) 是由 \(C_x\) 的特征向量组成的矩阵,它的第一行表示最大特征值对应的特征向量,第二行表示第二大特征值对应的特征向量。\(C_y\) 对角线上的 \(\lambda_k\) 代表 \(C_x\) 的特征值,而且是按照从大到小排序的(\(\lambda_1 > \lambda_2 > \dots > \lambda_n\))。
这个新的协方差矩阵有一个很重要的性质,除了对角线上的元素,其他元素通通是 0。要知道,协方差矩阵中,对角线上的元素表示方差,非对角线上的元素表示协方差。这说明,经过 PCA 处理后,我们把原本的数据 \(x\),转变成各个分量之间没有任何关系(协方差为 0)的数据 \(y\)!我认为这正是 PCA 的精髓所在,也是我们使用 PCA 算法的根本目标。
另外,PCA 还经常用于降维处理,那么为什么 PCA 的降维效果会那么好?
首先要明确一点,降维不是随便都能降的,最好的降维方法是要尽量保留重要的信息,而忽略次要的信息。在 PCA 中,我们一般是对协方差矩阵的特征值按从大到小排序,然后舍弃一些比较小的特征值(以及这些特征值对应的特征向量),这样重新计算得到 \(y\) 后,它的协方差矩阵可能是这个样子的: \[ C_y=\begin{bmatrix} \lambda_1 & & & 0 \\ & \lambda_2 & & \\ & & \ddots & \\ 0 & & & \lambda_k \end{bmatrix} \] (我们舍弃掉了 \(n-k\) 个特征向量,将数据由 \(n\) 维降到 \(k\) 维)
要知道,这些特征值(或者说方差)都是按照从大到小排序的,也就是说,我们在降维时,舍弃掉了那些特征值比较小的分量。这么做是符合常理的,因为数据的方差越大,证明分布越广,这样,我们还原这些数据的难度是越大的,而方差越小,证明数据分布越集中,还原它们的难度就越小(方差为 0 的话,用一个数就可以代表所有样本了)。所以,降维时,我们尽量保留那些方差大的数据,而忽略那些方差小的。本文开篇的图中给出一个形象的解释,我们把一个二维的数据映射到一维时,也是优先映射到方差大的那一维上,这样,原数据的分布规律可以最大限度的保留下来,信息的保留也是最完整的。