最近在学习 SVM 的过程中,遇到关于优化理论中拉格朗日乘子法的知识,本文是根据几篇文章总结得来的笔记。由于是刚刚接触,难免存在错误,还望指出😁。另外,本文不会聊到深层次的数学推导,仅仅是介绍拉格朗日乘子法的内容,应用,以及个人对它的感性理解。
什么是拉格朗日乘子法
按照维基百科的定义,拉格朗日乘数法是一种寻找多元函数在其变量受到一个或多个条件的约束时的极值的方法。用数学式子表达为: \[ \underset{x, y} {\operatorname {minimize}} f(x, y) \\ \operatorname{subject\ to} g(x, y) = c \] 简单理解就是,我们要在满足 \(g(x, y)=c\) 这个等式的前提下,求 \(f(x, y)\) 函数的最小值(最大值道理相同)。这样的问题我们在高中的时候就遇到过了,只不过高中时遇到的限制条件 \(g(x, y)=c\) 都比较简单,一般而言都可以将 \(y\) 用 \(x\) 的式子表示出来,然后用变量替换的方法代回 \(f(x, y)\) 求解。但是,如果 \(g(x, y)\) 的形式过于复杂,或者变量太多时,这种方法就失效了。而拉格朗日乘子法就是解决这类问题的通用策略。
拉格朗日乘子法的原理
一个约束条件
我们先从只有一个约束条件的情况入手,看看拉格朗日乘子法到底是怎么做的。
假设,我们的问题如下: \[ \underset{x,y} {\operatorname{minimize}} f(x, y)=x^2+y^2 \\\\ {\operatorname {subject to}}\ g(x, y)=xy-1=0 \] 当然,这个问题比较简单,直接用 \(g(x, y)\) 解出 y 再代入 \(f(x, y)\) 也可以求解,但这里,我们准备用拉格朗日乘子法。
首先我们画出 \(f(x, y)\) 的图像,这个图像应该是 3 维的,但为了方便讲解,这里给出它的 2 维投影:
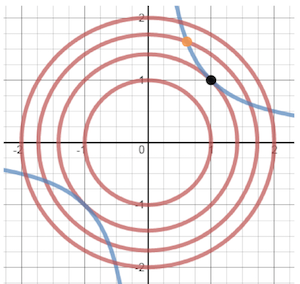
图中的红色圆表示 \(f(x, y)\),越靠近原点的部分,值越小(表示“谷底”),这些圆又称为「等高线」,因为同一个圆代表的函数值相同。
图中的蓝线代表 \(g(x, y)\),这里只取 \(g(x, y)=0\) 的部分。
整幅图像可以想象成一个巨大的山谷,原点是谷底,而我们的任务是在蓝线表示的道路上,找到最低的位置。
那要如何找到这个最低点呢?注意,图中用橙色和黑色标记了两个点。如果我们走到了橙色这个位置,那么很明显,可以发现这个点肯定不是最低的,因为我们可以沿着蓝线继续往内部的圆走,当我们走到黑色这个点时,会发现没法再往里面走了,而且,这个时候如果继续沿蓝线走,我们的位置反而升高了,这时,我们基本可以认为:我们找到了在蓝线这个限制条件下的最低点。
那么橙色这个点和黑色这个点有什么本质区别呢?拉格朗日观察到,黑点位置,蓝线和圆是相切的,而橙点位置显然不满足这个性质。那相切是否是必然的呢?拉格朗日告诉我们,是的,一定是相切的。而这一点,正是拉格朗日乘子法的核心。
梯度
在正式理解拉格朗日乘子法的原理之前,我们要回顾一下梯度的概念。
在数学里面,梯度指的是函数变化最快的方向。例如:在一元函数 \(f(x)\) 中,梯度只能沿 x 轴正方向或负方向,而在二元函数 \(f(x,y)\) 中,梯度则是一个二维向量 \((\partial f/\partial x,\partial f/\partial y)\)。
现在,我们要用到梯度一个重要的性质:梯度跟函数等高线是垂直的。
证明需要用到一点极限的知识。
梯度的数学定义为:\(\nabla f=(\partial f / \partial x, \partial f / \partial y)\)。假设 \(\Delta x\),\(\Delta y\) 是两个极小的变化量,根据全微分的知识,可以得到: \[ f(x+\Delta x, y+\Delta y) \approx f(x, y)+\frac{\partial f}{\partial x}\Delta x + \frac{\partial f}{\partial y}\Delta y \] 如果 \((\Delta x, \Delta y)\) 是在等高线方向的增量,那么 \(f(x+\Delta x, y+\Delta y) \approx f(x, y)\),这意味着 \(\frac{\partial f}{\partial x}\Delta x + \frac{\partial f}{\partial y}\Delta y=0\),换句话说,向量 \(\nabla f\) 和向量 \((\Delta x, \Delta y)\) 的内积为 0。所以,梯度和函数的等高线是垂直的。
拉格朗日乘子法的几何认识
现在,我们来感性地认识一下,为什么拉格朗日认为相切才能找到最低点(只是感性认识,不添加任何数学推导)。
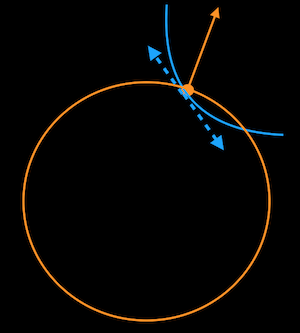
在橙点这个位置,由于两条曲线不相切,所以橙线的梯度(上图橙色箭头)和蓝线的切线(蓝色虚线)肯定不垂直。在这种情况下,蓝线的两个切线方向,必定有一个往函数高处走(与梯度的夹角小于 90 度),有一个往函数低处走(与梯度的夹角大于 90 度)。所以,在两条曲线相交时,我们肯定不在最低点或最高点的位置。
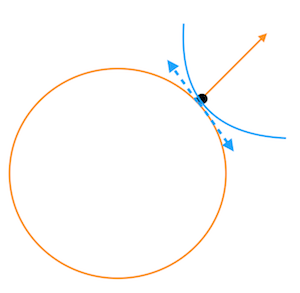
那么,反过来想,如果两条曲线相切(上图),那么在切点这个位置,蓝线的切线和橙线的梯度是垂直的,这个时候,蓝线的切线方向都指向橙线的等高线方向。换句话说,在切点的位置沿蓝线移动很小的一步,都相当于在橙线的等高线上移动,这个时候,可以认为函数值已经趋于稳定了。所以,我们认为这个点的值“可能”是最低(高)的(之后解释为什么是“可能“。另外,个人觉得拉格朗日乘子法最好用反证法从不相切的点入手思考,从相切的点思考总有点别扭)。
既然相切可以帮助我们找到最低点,那么接下来我们要研究的便是如何利用相切来找出最低点。
相切,意味着在切点的位置,两条曲线的等高线方向是平行的,考虑到梯度与等高线垂直, 我们可以用两条曲线的梯度平行来求出切点位置(最低点)。
因此,根据梯度平行,我们能够得到一个方程组:\(\nabla f = \lambda \nabla g\),其中 \(\lambda\) 表示一个标量,因为我们虽然能保证两个梯度平行,但不能保证它们的长度一样(或者方向相同)。在高维函数中,\(\nabla f\) 表示的是函数在各个自变量方向的偏导。对于上面的例子,我们可以求出函数 \(f\) 和 \(g\) 的偏导,再根据方程组: \[ \frac{\partial f}{\partial x}= \lambda \frac{\partial g}{\partial x} \\\\ \frac{\partial f}{\partial y}=\lambda \frac{\partial g}{\partial y} \\\\ g(x,y)=0 \] 求出切点。由于总共有三个方程和三个未知数,一般都能找到解(也可能存在多个解或无解的情况,之后会简单讨论)。
在实际求解时,人们会使用一个统一的拉格朗日函数:\(L(x,y,\lambda)=f(x,y)+\lambda g(x,y)\),令这个函数偏导为 0,我们可以得到: \[ \partial L/ \partial x=\frac{\partial f} {\partial x}- \lambda \frac{\partial g}{\partial x}=0 \\\\ \partial L/ \partial y=\frac{\partial f}{\partial y}- \lambda \frac{\partial g}{\partial y}=0 \\\\ \partial L/ \partial \lambda=g(x,y)=0 \] 结果和上面的方程组是一样的。
多个约束条件
多个约束条件和单个约束条件是一样的。如果是多个约束条件,那么这些约束函数肯定是相交的,否则无解。多个约束条件一般会把变量约束到一个更低维的空间,例如,下图中,紫色球面和黄色平面将变量约束到黑色线的位置。

求解过程和单个约束条件是一样的,我们定义一个新的拉格朗日函数: \[ L(x_1,\dots,x_n,\lambda_1,\dots,\lambda_k)=f(x_1,\dots,x_n)-\sum_{j=1}^k{\lambda_j g_j(x_1,\dots,s_n)} \] 然后同样令这个函数的导数 \(\nabla L=0\),最后可以得到 \(n+k\) 个方程以及 \(n+k\) 个未知数,一般也能求解出来。
总结
根据拉格朗日乘子法的定义,这是一种寻找极值的策略,换句话说,该方法并不能保证找到的一定是最低点或者最高点。事实上,它只是一种寻找极值点的过程,而且,拉格朗日乘子法找到的切点可能不只一个(也就是上面的方程组可能找到多个解),例如下图:
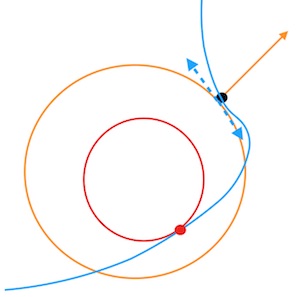
图中相切的点有两个,而红点的函数值明显比黑点小。事实上,要想判断找到的点是极低点还是极高点,我们需要将切点代入原函数再进行判断。
另外,在写作本文时,我仍然有一个疑惑没有解决:拉格朗日乘子法在哪些情况下无解(也就是上面的方程组 \(\nabla L\) 无解)?换句话说,约束条件和函数没有切点时,我们要怎么求出最低点或最高点。这个问题留待之后想通再补上。