今天分享的这篇论文是 SIGGRAPH 2015 的入选论文,标题比较长,但它做的事情其实很简单:通过一张图片,找到和这张图片最相似的 3D 形状👇。

论文的思路
一开始看到论文的结果图的时候,觉得这个想法还是很有新意的。由于我刚刚踏入图形学的领域,对这类技术的认识还比较肤浅,就在网上搜了下相关的内容,发现十多年前就已经有人在研究相关的算法了。有利用 3D 形状的拓扑性质的,有提取一些特征算子的,也有通过图像检索的。总的来说,3D 形状的检索已经是一个较老的话题了。这篇论文也是从图像检索的角度出发,结合 3D 模型的投影图像,创造性地将图像和形状融合进一个空间中。通过空间中的点之间的距离,可以很方便地计算出图像与形状的相似度。
论文最主要的工作就是构造一个可以嵌套图像和形状的空间。要将 3D 和 2D 统一在一起,难度是比较大的。一般来说,3D 模型包含的信息更多,而图像方面的技术则比较成熟。因此,论文选择找一块「二向箔」将 3D 投影成 2D 后,再通过图像特征提取技术构造出这个空间。
具体流程分为四步:
- 构造形状嵌套空间(Shape Embedding Space);
- 合成训练图片(训练 CNN);
- 通过 CNN 将图片映射进 Shape Embedding Space;
- 输入图片预测 3D 模型。
Embedding Space Construction
第一步,我们先根据 3D 模型构造出这个空间。
Shape Similarity
在构造出这个空间之前,我们先思考一下,3D 模型之间的相似度要怎么测量?
前面说了,论文是通过将 3D 形状投影成图像的方法,将该问题转化为我们熟悉的图像相似度的比较。
假设我们有一个 3D 模型的集合(这里面可能包括椅子、桌子、飞机等,参考上图):\(S={\lbrace S_i \rbrace}_{i=1}^{n}\)。这个集合里的模型形状要事先做好对齐。
然后,我们从 k 个不同的视角(viewpoint)对各个模型进行投影,得到每个模型的投影图片集合:\(I_i={\lbrace I_{i,v} \rbrace}_{v=1}^{k} \ \ for\ each \ \ S_i\)。论文中 k 取 20。
接着,对于每张投影图片 \(I_i\),提取图片的 HoG 特征:\(H_{i, v} \in R^{10188}\)。这里提取的 HoG 特征由三个尺寸的图像特征组合而成:120x120,60x60,30x30。将每个尺寸下的 HoG 特征组合在一起,形成一个 10188 维的向量。由于 3D 形状事先已经对齐了,所以 HoG 在鲁棒性上得到了保证。
对于每一个形状 \(S_i\),我们组合所有投影图片的 HoG 特征(这个特征又称为 LightField HoG),得到形状本身的特征 \(F_i=(H_{i,1}; H_{i,2}; …; H_{i,k}) \in R^{203760}\),这个特征的维度为 203760(10188 x 20)。对于两个不同形状间的相似度比较,可以由这个特征向量的欧氏距离计算得到:\(d_{i,j}=||F_i - F_j||_2\)。
Embedding Space
有了这个基本的相似度计算方法后,我们可以开始着手构建这个空间了。
论文中对这个空间提出了两点要求:
- 空间中的距离要能够体现相似性程度;
- 空间维度要尽可能低。
构造空间最简单的方法就是直接使用上面提出来的特征向量 \(F_i\),构造一个特征空间 \(F=\lbrace F_i \rbrace\)。这个特征空间的维度明显偏高(203760维),因此,论文中又使用 PCA 算法对特征向量进行降维,得到一个新的特征空间 \(F^{-}\),维度为 128 维。
但这个降维后的空间存在一个问题:虽然 \(F^{-}\) 能够表示形状之间的相似度,但却难以体现不相似度。换句话说,相似的形状之间的距离都很相近,但不相似的形状(比如:椅子和汽车)之间的距离则完全没有意义(可能很近也可能很远)。论文中的说法是:\(F^{-}\) does not respect this distinction between the greater importance of the samll distances and the lesser one of the larger ones. 由于我英语水平有限,对这句顺口溜不是特别理解,但不管怎样,\(F^{-}\) 是存在不足的。
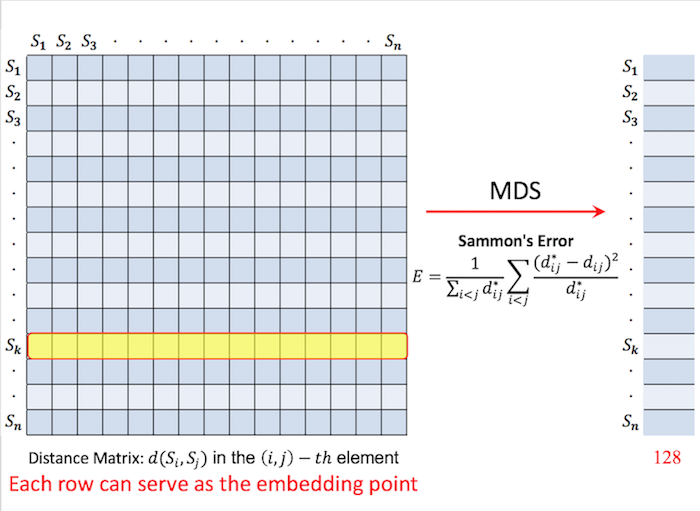
因此,论文提出一个新的空间 \(D_{n*n}\),代表一个距离矩阵:\(D(i, j) = d_{i, j}\)。由于 \(F\) 是原特征向量组成的空间,而 \(D\) 则是一个距离矩阵,因此,对 \(D\) 降维后,仍然可以很好地表达相似性和不相似性(这一点暂时不是很理解)。降维方面,作者比较了多种方法,最后发现,使用 non-linear Multi-Dimensional Scaling(MDS) 方法效果上最好。该方法的提出是在 1964 年,听起来相当的有格调又很有历史感,我暂时没有去了解,所以先姑且把它当作一个黑盒子吧。总之,我们通过这个方法,将距离矩阵 \(D_{n*n}\) 降维成 \(D^{-}\),维度同样保持 128 维(见下图)。然后,将降维后的矩阵 \(D^{-}\) 的行向量当作形状的特征向量。这种用距离来表示特征的方法我是第一次遇到,还不是很理解。作者在论文的 PPT 中这样解释:如果两个形状跟其他所有形状之间的 distance 差不多,也就是说它们在 \(D^{-}\) 的行向量很相似,那么这两个形状也应该是类似的。
CNN for Image Embedding
构造出 \(D^{-}\) 空间后,我们相当于把一个 3D 模型 \(S_i\) 映射到 \(D^{-}\) 中的一个点 \(P_{S_{i}}\)。下一步,就是要把图像也映射进这个空间,这相当于一个特征提取的工作,而 CNN 正是完成该工作的最佳选择之一。
我们的目标是训练一个 CNN 网络,这个网络的输入是一张图片,输出是一个向量 \(P_{I} \in D^{-}\)。要求是,如果图片 \(I\) 描述的是一个形状类似于 \(S_i\) 的物体,那么 \(P_{I}\) 要接近于 \(P_{S_{i}}\)。
Training Image Synthesis
这一步将准备合成训练图片。需要先明确一点,论文中用到的所有训练图片,都是对 3D 模型进行投影渲染合成的。换句话说,这些图片并不是真实世界中的物体图片。不过,由于论文中用到的 3D 模型在制作上都非常真实,因此这些模型渲染出来的图片和真实图片很相似。
由于我们是要把一张图片转换成一个特征向量,因此训练数据的格式应该是:(图片,向量)。由于之前构造空间 \(D^{-}\) 的时候,我们已经计算出了每个形状 \(S_i\) 对应的特征向量,因此,只需要对 \(S_i\) 各个角度的投影进行渲染得到一个图片集 \(R_i\),对于图片集中的每张图片 \(R_{i,r}\),我们相当于得到了一个训练样本 \((R_{i,r}, P_{S_{i}})\)。由于 CNN 容易过拟合,因此,除了生成大量训练样本外,论文还在渲染投影图片的时候,加入一些额外的「噪声」,比如:添加不同的光照、采用多个角度进行投影,以及融合一些随机背景等。
论文中总共生成了约 100 万张训练图片。
Network Architecture and Training
论文中直接采用了 AlexNet 的架构,唯一不同的只是将网络最后一层 fc8 的输出改为 128 维的向量(原 AlexNet 是将 fc8 输入到 softmax 层),同时将 Softmax Loss Layer 换成 Euclidean Loss Layer。这个损失函数具体为:
\(L(\theta)=\sum_{i,r}{||f(R_{i,r}; \theta) - P_{S_{i}}||_{2}^{2}}\)
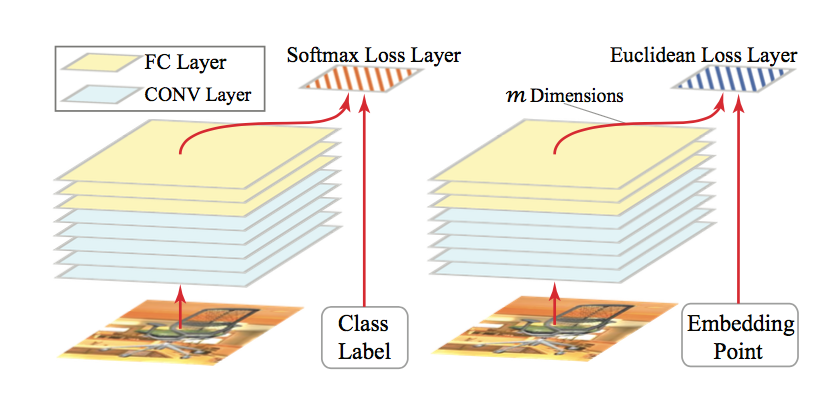
上图中,左图为原来的 AlexNet,右图为论文中采用的 CNN。
由于真实环境的照片中,背景会更加复杂,因此,网络前面五层卷积层的参数直接使用其他人在 ImageNet 上训练好的参数。而网络后面三层全连接层 FC Layer,则将参数随机初始化,并用之前生成的数据进行训练,这样,每次梯度下降的时候只优化后面三层网络的参数。这个过程又被称为 fine-tune。
作者称这个 CNN 的工作为 purifying,译为「清理」的意思。也就是说,CNN 可以把图片中一些无关的背景等噪音剔除出去,识别出物体特有的特征向量。
Predicting
预测的时候,我们需要将图片输入到 CNN 中,得到一个特征向量。然后在 \(D^{-}\) 空间内,用 KNN 之类的方法找到距离最近的向量,这些向量对应的形状就是图片中的物体最相似的形状。而如果要用形状来检索,则需要先把形状投影成图片后,再放入 CNN 中,然后用同样的方法找到最相似的形状。另外,这个空间还可以用来以图搜图,只要将所有图片都输入到 CNN 中,找出它们在空间中的位置,根据欧氏距离就可以判断出最相似的图片了。个人觉得这一点正是这个形状嵌套空间的优势所在。
实验结果及应用
论文从多角度图片检索(cross-view image retrieval)、基于图片的形状检索,以及基于形状的图片检索上,和其他方法进行了对比,结果均有提高。当然,针对不同的形状模型,提高的幅度也是不尽相同。
我更感兴趣的是这个东西有哪些应用。
最容易想到的,自然是 3D 模型以及图片的检索上。而且,由于论文构造的空间将 3D 和 2D 融合在一起,因此,对以图搜形,以形搜图、以图搜图、以形搜形来说,都是通用的。不过,由于 CNN 只接收图片作为输入,如果想用形状来检索,就必须先把形状投影成图片才行。
论文还提到另一种好玩的应用 Shape-Guided Image Editing。

比如,我们想在图片中为椅子增加一个台灯照射下的阴影效果,这个时候,直接基于图像处理的方法是比较难做到的,而换个角度,可以先用一个类似的 3D 模型投射出这个阴影后,再把阴影加入到原图中。