由之前的文章我们可以得到贝塞尔曲线的方程,今天要通过贝塞尔曲线(三次)重新推出控制点。
需求
在得到并对贝塞尔曲线做完处理后,为了让浏览器重新渲染贝塞尔曲线,必须通过贝塞尔曲线重新取得控制点坐标。
准备条件
了解 SVG 的 path 中 C/c 相关指令的用法,还有相对位置等一些概念。最好能提前获得贝塞尔曲线的表达式。
解决方案
假设我们已经得到了贝塞尔曲线的表达式: \[ \overline{P^3} = (1-t)^3\overline{P_{0}} + 3t(1-t)^2\overline{P_{1}}+3t^2(1-t)\overline{P_{2}}+t^3\overline{P_{3}} \tag{1} \] 其中,$ $ 是三次贝塞尔曲线上的点,\(\overline{P_{0}}\)、\(\overline{P_{1}}\)、\(\overline{P_{2}}\)、\(\overline{P_{3}}\) 分别是贝塞尔曲线的控制点,因为 \(\overline{P_{0}}\)、\(\overline{P_{3}}\) 本身就是贝塞尔曲线的两个端点,所以它们的坐标是事先知道的,我们的目标是要求出 \(\overline{P_{1}}\)、\(\overline{P_{2}}\)。注意到,贝塞尔曲线的点是 t 由 0 逐渐增加到 1 的过程中采样得到的(数学上需要对 t 取极限,但计算机是离散的,所以称为采样),因为项目中,我是通过原控制点得到贝塞尔曲线后,对曲线做形变处理,然后再反推控制点,所以我只需要在原来的贝塞尔曲线表达式中分别取 t=\(\frac{1}{3}\) 和 \(\frac{2}{3}\) ( t 的取值可以是 0 到 1 之间任意实数,当然不能是 0 和 1,不然就和端点重合了),就可以得到两个 \(\overline{P^3}\) 点的坐标,形变处理完后,我同样近似地认为这两个点是新曲线中 t 取 \(\frac{1}{3}\) 和 \(\frac{2}{3}\) 的坐标点。这样,我们相当于知道了四个点的坐标,对于一个二元一次方程,我们由这四个点可以得到两组方程,最终一定可以把 \(\overline{P_{1}} 、\overline{P_{2}}\) 解出来。对于原表达式不知道的情况,可以根据端点坐标来近似取点,具体可以看参考链接。
step1
对于 (1) 式,令 t=\(\frac{1}{3}\),我们得到: \[ \overline{P^3}=(\frac{2}{3})^3\overline{P_{0}}+(\frac{2}{3})^2\overline{P_{1}}+3(\frac{1}{3})^2\frac{2}{3}\overline{P_{2}}+(\frac{1}{3})^3\overline{P_{3}} \] \[ \overline{P^3}-\frac{8}{27}\overline{P_{0}}-\frac{1}{27}\overline{P_{3}}=\frac{4}{9}\overline{P_{1}}+\frac{2}{9}\overline{P_{2}} \tag{2} \]
因为 \(\overline{P^3}\)、\(\overline{P_{0}}\)、\(\overline{P_{3}}\) 的坐标是事先已知的,所以可以设 \(\overline{P^3}-\frac{8}{27}\overline{P_{0}}-\frac{1}{27}\overline{P_{3}}\) 为 \(\overline{B}\)。我们设 \(\overline{P_{1}}\)、\(\overline{P_{2}}\) 的坐标分别为 (x1, y1)、(x2, y2),\(\overline{B}\) 的坐标为(\(x_{b}\), \(y_{b}\)),由 (2) 式可以得到如下方程: \[ \frac{4}{9}x_{1}+\frac{2}{9}x_{2}=x_{b} \]
\[ \frac{4}{9}y_{1}+\frac{2}{9}y_{2}=y_{b} \]
step2
按照 step1 的思路,令 t=\(\frac{2}{3}\),可以得到: \[ \overline{P^3}-\frac{1}{27}\overline{P_{0}}-\frac{8}{27}\overline{P_{3}}=\frac{2}{9}\overline{P_{1}}+\frac{4}{9}\overline{P_{2}} \tag{3} \] 令 \(\overline{P^3}-\frac{1}{27}\overline{P_{0}}-\frac{8}{27}\overline{P_{3}}\) 为 \(\overline{C}\),设 \(\overline{C}\) 的坐标为 (\(x_{c}\), \(y_{c}\)),同样的可以得到另一组方程: \[ \frac{2}{9}x_{1}+\frac{4}{9}x_{2}=x_{c} \]
\[ \frac{2}{9}y_{1}+\frac{4}{9}y_{2}=y_{c} \]
step3
联立 step1 和 step2 的方程组,最终可以吧 \(\overline{P_{1}}\)、\(\overline{P_{2}}\) 的坐标求出来。 \[ x_{1}=3x_{b}-\frac{3}{2}x_{c} \]
\[ y_{1}=3y_{b}-\frac{3}{2}y_{c} \]
\[ x_{2}=3x_{c}-\frac{3}{2}x_{b} \]
\[ y_{2}=3y_{c}-\frac{3}{2}y_{b} \]
代码实现
1 | /** |
测试结果
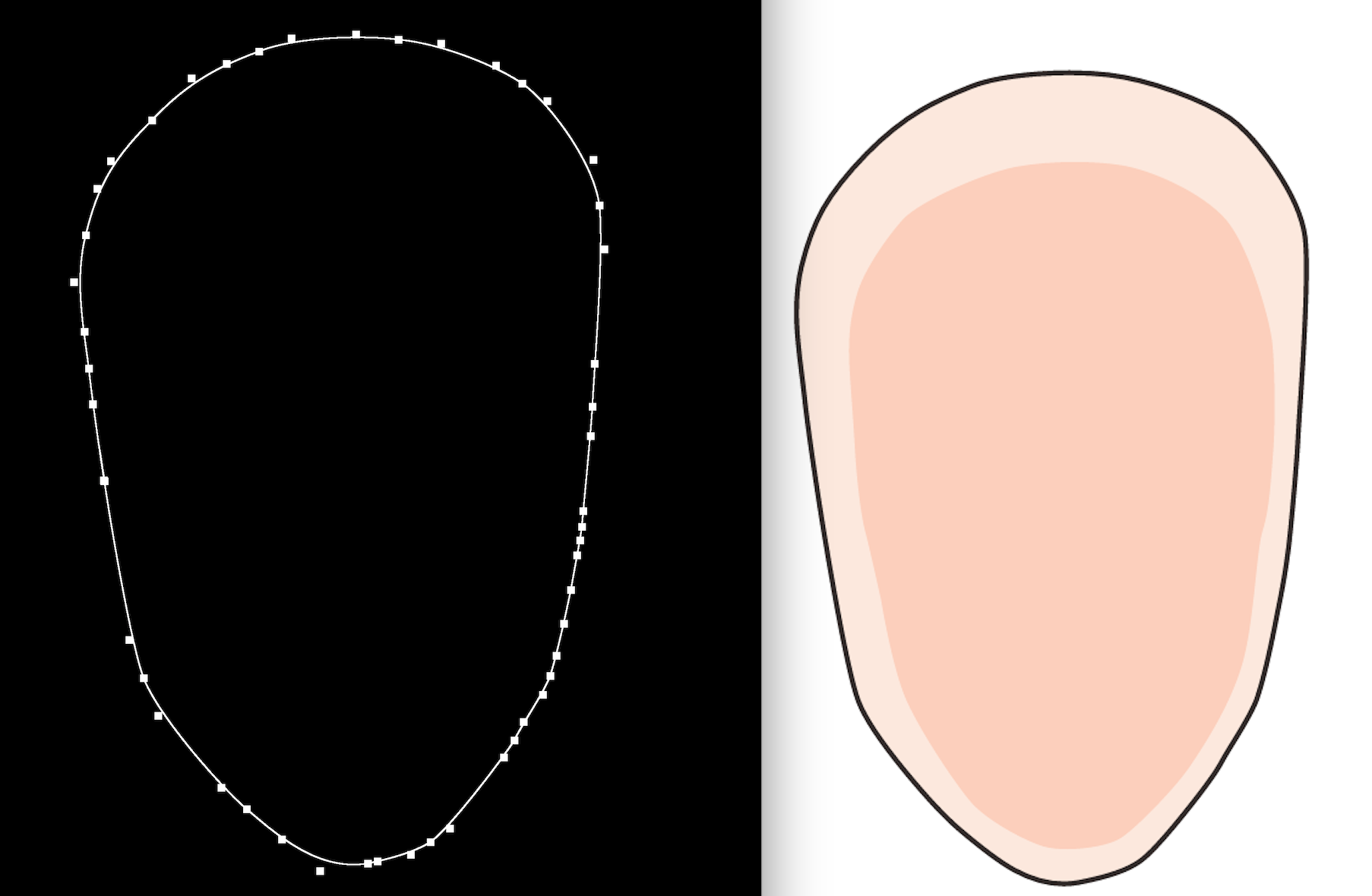
右图的脸为原 svg 在浏览器中的展示效果,左图的脸部轮廓白点为根据 svg 的控制点绘制出贝塞尔曲线后,再根据贝塞尔曲线反推的控制点坐标,而左图的脸部曲线则是根据这些控制点绘制出的贝塞尔曲线。从效果上看,两张人脸的轮廓基本很相似。
接下来,我对贝塞尔曲线做了平移、缩放和旋转,看看重新推出的控制点以及贝塞尔曲线的情况:
平移操作

缩放操作

旋转操作

看得出,这些基本的线性变换都不会导致贝塞尔曲线「失真」:-),这是个好消息。
参考
Algorithm for deriving control points of a bezier curve from points along that curve?